


Here, I begin the technical description of the basics of loop
quantum gravity. The starting point of the construction of the
quantum theory is classical general relativity, formulated in
terms of the Sen-Ashtekar-Barbero connection [190 ,
7,
40
,
7,
40 ]. Detailed introductions to the (complex) Ashtekar formalism can
be found in the book [9
]. Detailed introductions to the (complex) Ashtekar formalism can
be found in the book [9 ], in the review article [164], and in the conference proceedings [81]. The real version of the theory is presently the most widely
used.
], in the review article [164], and in the conference proceedings [81]. The real version of the theory is presently the most widely
used.
Classical general relativity can be formulated in phase space
form as follows [9 ,
40]. We fix a three-dimensional manifold
M
(compact and without boundaries) and consider a smooth real
SU
(2) connection
,
40]. We fix a three-dimensional manifold
M
(compact and without boundaries) and consider a smooth real
SU
(2) connection
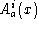 and a vector density
and a vector density
 (transforming in the vector representation of
SU
(2)) on
M
. We use
(transforming in the vector representation of
SU
(2)) on
M
. We use
 for spatial indices and
for spatial indices and
 for internal indices. The internal indices can be viewed as
labeling a basis in the Lie algebra of
SU
(2) or in the three axis of a local triad. We indicate
coordinates on
M
with
x
. The relation between these fields and conventional metric
gravitational variables is as follows:
for internal indices. The internal indices can be viewed as
labeling a basis in the Lie algebra of
SU
(2) or in the three axis of a local triad. We indicate
coordinates on
M
with
x
. The relation between these fields and conventional metric
gravitational variables is as follows:
 is the (densitized) inverse triad, related to the
three-dimensional metric
is the (densitized) inverse triad, related to the
three-dimensional metric
 of constant-time surfaces by
of constant-time surfaces by

where
g
is the determinant of
 ; and
; and

 is the spin connection associated to the triad, (defined by
is the spin connection associated to the triad, (defined by
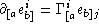 , where
, where
 is the triad).
is the triad).
 is the extrinsic curvature of the constant time three
surface.
is the extrinsic curvature of the constant time three
surface.
In (2 ),
),
 is a constant, denoted the Immirzi parameter, that can be chosen
arbitrarily (It will enter the hamiltonian constraint.) [114,
115,
116]. Different choices for
is a constant, denoted the Immirzi parameter, that can be chosen
arbitrarily (It will enter the hamiltonian constraint.) [114,
115,
116]. Different choices for
 yield different versions of the formalism, all equivalent in the
classical domain. If we choose
yield different versions of the formalism, all equivalent in the
classical domain. If we choose
 to be equal to the imaginary unit,
to be equal to the imaginary unit,
 , then
A
is the standard Ashtekar connection, which can be shown to be
the projection of the selfdual part of the four-dimensional spin
connection on the constant time surface. If we choose
, then
A
is the standard Ashtekar connection, which can be shown to be
the projection of the selfdual part of the four-dimensional spin
connection on the constant time surface. If we choose
 , we obtain the real Barbero connection. The hamiltonian
constraint of Lorentzian general relativity has a particularly
simple form in the
, we obtain the real Barbero connection. The hamiltonian
constraint of Lorentzian general relativity has a particularly
simple form in the
 formalism; while the hamiltonian constraint of Euclidean general
relativity has a simple form when expressed in terms of the
formalism; while the hamiltonian constraint of Euclidean general
relativity has a simple form when expressed in terms of the
 real connection. Other choices of
real connection. Other choices of
 are viable as well. In particular, it has been argued that the
quantum theory based on different choices of
are viable as well. In particular, it has been argued that the
quantum theory based on different choices of
 are genuinely physical inequivalent, because they yield
``geometrical quanta'' of different magnitude [189
are genuinely physical inequivalent, because they yield
``geometrical quanta'' of different magnitude [189 ]. Apparently, there is a unique choice of
]. Apparently, there is a unique choice of
 yielding the correct 1/4 coefficient in the Bekenstein-Hawking
formula [134
yielding the correct 1/4 coefficient in the Bekenstein-Hawking
formula [134 ,
135
,
135 ,
176
,
176 ,
11
,
11 ,
178
,
178 ,
70
,
70 ], but the matter is still under discussion.
], but the matter is still under discussion.
The spinorial version of the Ashtekar variables is given in
terms of the Pauli matrices
 , or the
su
(2) generators
, or the
su
(2) generators
 , by
, by

Thus,
 and
and
 are
are
 anti-hermitian complex matrices.
anti-hermitian complex matrices.
The theory is invariant under local
SU
(2) gauge transformations, three-dimensional diffeomorphisms of
the manifold on which the fields are defined, as well as under
(coordinate) time translations generated by the hamiltonian
constraint. The full dynamical content of general relativity is
captured by the three constraints that generate these gauge
invariances [190,
9].
As already mentioned, the Lorentzian hamiltonian constraint
does not have a simple polynomial form if we use the real
connection (2 ). For a while, this fact was considered an obstacle to defining
the quantum hamiltonian constraint; therefore the complex version
of the connection was mostly used. However, Thiemann has recently
succeeded in constructing a Lorentzian quantum hamiltonian
constraint [206
). For a while, this fact was considered an obstacle to defining
the quantum hamiltonian constraint; therefore the complex version
of the connection was mostly used. However, Thiemann has recently
succeeded in constructing a Lorentzian quantum hamiltonian
constraint [206 ,
201
,
201 ,
202
,
202 ] in spite of the non-polynomiality of the classical expression.
This is the reason why the real connection is now widely used.
This choice has the advantage of eliminating the old ``reality
conditions'' problem, namely the problem of implementing
non-trivial reality conditions in the quantum theory.
] in spite of the non-polynomiality of the classical expression.
This is the reason why the real connection is now widely used.
This choice has the advantage of eliminating the old ``reality
conditions'' problem, namely the problem of implementing
non-trivial reality conditions in the quantum theory.




|
Loop Quantum Gravity
Carlo Rovelli
http://www.livingreviews.org/lrr-1998-1
© Max-Planck-Gesellschaft. ISSN 1433-8351
Problems/Comments to
livrev@aei-potsdam.mpg.de
|
 ,
40]. We fix a three-dimensional manifold
M
(compact and without boundaries) and consider a smooth real
SU
(2) connection
,
40]. We fix a three-dimensional manifold
M
(compact and without boundaries) and consider a smooth real
SU
(2) connection
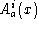 and a vector density
and a vector density
 (transforming in the vector representation of
SU
(2)) on
M
. We use
(transforming in the vector representation of
SU
(2)) on
M
. We use
 for spatial indices and
for spatial indices and
 for internal indices. The internal indices can be viewed as
labeling a basis in the Lie algebra of
SU
(2) or in the three axis of a local triad. We indicate
coordinates on
M
with
x
. The relation between these fields and conventional metric
gravitational variables is as follows:
for internal indices. The internal indices can be viewed as
labeling a basis in the Lie algebra of
SU
(2) or in the three axis of a local triad. We indicate
coordinates on
M
with
x
. The relation between these fields and conventional metric
gravitational variables is as follows:
 is the (densitized) inverse triad, related to the
three-dimensional metric
is the (densitized) inverse triad, related to the
three-dimensional metric
 of constant-time surfaces by
of constant-time surfaces by



 ; and
; and
 is the spin connection associated to the triad, (defined by
is the spin connection associated to the triad, (defined by
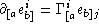 , where
, where
 is the triad).
is the triad).
 is the extrinsic curvature of the constant time three
surface.
is the extrinsic curvature of the constant time three
surface.
 is a constant, denoted the Immirzi parameter, that can be chosen
arbitrarily (It will enter the hamiltonian constraint.) [
is a constant, denoted the Immirzi parameter, that can be chosen
arbitrarily (It will enter the hamiltonian constraint.) [ , then
A
is the standard Ashtekar connection, which can be shown to be
the projection of the selfdual part of the four-dimensional spin
connection on the constant time surface. If we choose
, then
A
is the standard Ashtekar connection, which can be shown to be
the projection of the selfdual part of the four-dimensional spin
connection on the constant time surface. If we choose
 , we obtain the real Barbero connection. The hamiltonian
constraint of Lorentzian general relativity has a particularly
simple form in the
, we obtain the real Barbero connection. The hamiltonian
constraint of Lorentzian general relativity has a particularly
simple form in the
 , or the
su
(2) generators
, or the
su
(2) generators
 , by
, by
 and
and
 are
are
 anti-hermitian complex matrices.
anti-hermitian complex matrices.
