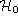of
is formed by states invariant under
SU
(2) gauge transformations. We now define an orthonormal basis in
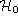. This basis represents a very important tool for using the
theory. It was introduced in [187
] and developed in [31,
32]; it is denoted spin network basis.
First, given a loop
in
M, there is a normalized state
in
, which is obtained by taking
and
f
(g)=-
Tr
(g). Namely
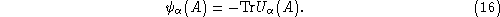
We introduce a Dirac notation for the abstract states, and
denote this state as
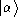. These sates are called loop states. Using Dirac notation, we
can write
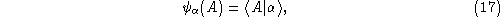
It is easy to show that loop states are normalizable. Products
of loop states are normalizable as well. Following tradition, we
denote with
also a multiloop, namely a collection of (possibly overlapping)
loops
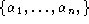, and we call
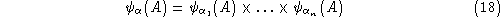
a multiloop state. (Multi-)loop states represented the main
tool for loop quantum gravity before the discovery of the spin
network basis. Linear combinations of multiloop states
(over-)span
, and therefore a generic state
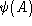is fully characterized by its projections on the multiloop
states, namely by
The ``old'' loop representation was based on representing
quantum states in this manner, namely by means of the functionals
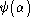over loop space defined in(19
). Equation (19) can be explicitly written as an integral transform, as we will
see in section
6.7
.
Next, consider a graph
. A ``coloring'' of
is given by the following.
. Equivalently, we may associate to each link
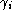a half integer number
, the spin of the irreducible, or, equivalently, an integer
number
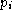, the ``color''
.
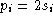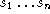, to each node of
in which links with spins
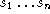meet. An invariant tensor is an object with
n
indices in the representations
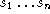that transform covariantly. If
n
=3, there is only one invariant tensor (up to a multiplicative
factor), given by the Clebsh-Gordon coefficient. An invariant
tensor is also called an
intertwining tensor
. All invariant tensors are given by the standard
Clebsch-Gordon theory. More precisely, for fixed
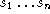, the invariant tensors form a finite dimensional linear
space. Pick a basis
is this space, and associate one of these basis elements to
the node. Notice that invariant tensors exist only if the
tensor product of the representations
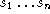contains the trivial representation. This yields a condition
on the coloring of the links. For
n
=3, this is given by the well known Clebsh-Gordan condition:
Each color is not larger than the sum of the other two, and the
sum of the three colors is even.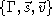
, or simply
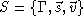, and denote it a ``spin network''. (It was Penrose who first
had the intuition that this mathematics could be relevant for
describing the quantum properties of the geometry, and who gave
the first version of spin network theory [152,
153].)
Given a spin network
S, we can construct a state
as follows. We take the propagator of the connection along each
link of the graph, in the representation associated to that link,
and then, at each node, we contract the matrices of the
representation with the invariant tensor. We obtain a state
, which we also write as
One can then show the following.
].
(choosing the basis of invariant tensors appropriately).] for details.The spin network states defined above are
SU
(2) gauge invariant. There exists also an extension of the spin
network basis to the full Hilbert space (see for instance [17,
51], and references therein).
|
Loop Quantum Gravity
Carlo Rovelli http://www.livingreviews.org/lrr-1998-1 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de |
