


A diagrammatic representation for the states in
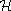 is very useful in concrete calculations. First, associate to a
loop state
is very useful in concrete calculations. First, associate to a
loop state
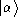 a diagram in
M, formed by the loop
a diagram in
M, formed by the loop
 itself. Next, notice that we can
multiply
two loop states, obtaining a normalizable state. We represent
the product of
n
loop states by the diagram formed by the set of the
n
(possibly overlapping) corresponding loops (we denote this set
``multiloop''). Thus, linear combinations of multiloops diagrams
represent states in
itself. Next, notice that we can
multiply
two loop states, obtaining a normalizable state. We represent
the product of
n
loop states by the diagram formed by the set of the
n
(possibly overlapping) corresponding loops (we denote this set
``multiloop''). Thus, linear combinations of multiloops diagrams
represent states in
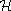 . Representing states as linear combinations of multiloops
diagrams makes computation in
. Representing states as linear combinations of multiloops
diagrams makes computation in
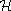 easy.
easy.
Now, the spin network state defined by the graph with no nodes
 , with color 1, is clearly, by definition, the loop state
, with color 1, is clearly, by definition, the loop state
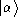 , and we represent it by the diagram
, and we represent it by the diagram
 . The spin network state
. The spin network state
 determined by the graph without nodes
determined by the graph without nodes
 , with color
n
can be obtained as follows. Draw
n
parallel lines along the loop
, with color
n
can be obtained as follows. Draw
n
parallel lines along the loop
 ; cut all lines at an arbitrary point of
; cut all lines at an arbitrary point of
 , and consider the
n
! diagrams obtained by joining the legs after a permutation. The
linear combination of these
n
! diagrams, taken with alternate signs (namely with the sign
determined by the parity of the permutation) is precisely the
state
, and consider the
n
! diagrams obtained by joining the legs after a permutation. The
linear combination of these
n
! diagrams, taken with alternate signs (namely with the sign
determined by the parity of the permutation) is precisely the
state
 . The reason for this key result can be found in the fact that
an irreducible representation of
SU
(2) can be obtained as the totally symmetric tensor product of
the fundamental representation with itself. For details, see [77
. The reason for this key result can be found in the fact that
an irreducible representation of
SU
(2) can be obtained as the totally symmetric tensor product of
the fundamental representation with itself. For details, see [77 ].
].
Next, consider a graph
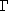 with nodes. Draw
with nodes. Draw
 parallel lines along each link
parallel lines along each link
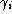 . Join pairwise the end points of these lines at each node (in
an arbitrary manner), in such a way that each line is joined with
a line from a different link (see Figure
1). In this manner, one obtains a multiloop diagram. Now
antisymmetrize the
. Join pairwise the end points of these lines at each node (in
an arbitrary manner), in such a way that each line is joined with
a line from a different link (see Figure
1). In this manner, one obtains a multiloop diagram. Now
antisymmetrize the
 parallel lines along each link, obtaining a linear combination
of diagrams representing a state in
parallel lines along each link, obtaining a linear combination
of diagrams representing a state in
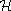 . One can show that this state is a spin network state, where
. One can show that this state is a spin network state, where
 is the color of the links, and the color of the nodes is
determined by the pairwise joining of the legs chosen [77
is the color of the links, and the color of the nodes is
determined by the pairwise joining of the legs chosen [77 ]. Again, simple
SU
(2) representation theory is behind this result.
]. Again, simple
SU
(2) representation theory is behind this result.
More in detail, if a node is trivalent (has 3 adjacent links),
then we can join legs pairwise only if the total number of the
legs is even, and if the number of the legs in each link is
smaller or equal than the sum of the number of the other two.
This can be recognized immediately as the Clebsch-Gordan
condition. If these conditions are satisfied, there is only a
single way of joining legs. This corresponds to the fact that
there is only one invariant tensor in the product of three
irreducible of
SU
(2). Higher valence nodes can be decomposed in trivalent
``virtual'' nodes, joined by ``virtual'' links. Orthogonal
independent invariant tensors are obtained by varying over all
allowed colorings of these virtual links (compatible with the
Clebsch-Gordan conditions at the virtual nodes). Different
decompositions of the node give different orthogonal bases. Thus
the total (links and nodes) coloring of a spin network can be
represented by means of the coloring of the real and the virtual
links. See Figure
1
.

Figure 1:
Construction of ``virtual'' nodes and ``virtual'' links over an
n
-valent node.
Vice versa, multiloop states can be decomposed in spin network
states by simply symmetrizing along (real and virtual) nodes.
This can be done particularly easily diagrammatically, as
illustrated by the graphical formulae in [187,
77 ]. These are standard formulae. In fact, it is well known that
the tensor algebra of the
SU
(2) irreducible representations admits a completely graphical
notation. This graphical notation has been widely used for
instance in nuclear and atomic physics. One can find it presented
in detail in books such as [214,
52,
66]. The application of this diagrammatic calculus to quantum
gravity is described in detail in [77
]. These are standard formulae. In fact, it is well known that
the tensor algebra of the
SU
(2) irreducible representations admits a completely graphical
notation. This graphical notation has been widely used for
instance in nuclear and atomic physics. One can find it presented
in detail in books such as [214,
52,
66]. The application of this diagrammatic calculus to quantum
gravity is described in detail in [77 ], which I recommend to anybody who intends to perform concrete
calculations in loop gravity.
], which I recommend to anybody who intends to perform concrete
calculations in loop gravity.
It is interesting to notice that loop quantum gravity was
first constructed in a pure diagrammatic notation, in [184 ]. The graphical nature of this calculus puzzled some, and the
theory was accused of being vague and strange. Only later did
researchers notice that the diagrammatic notation is actually
very conventional
SU
(2) diagrammatic calculus, well known in atomic and nuclear
physics.
]. The graphical nature of this calculus puzzled some, and the
theory was accused of being vague and strange. Only later did
researchers notice that the diagrammatic notation is actually
very conventional
SU
(2) diagrammatic calculus, well known in atomic and nuclear
physics.





|
Loop Quantum Gravity
Carlo Rovelli
http://www.livingreviews.org/lrr-1998-1
© Max-Planck-Gesellschaft. ISSN 1433-8351
Problems/Comments to
livrev@aei-potsdam.mpg.de
|
 , with color 1, is clearly, by definition, the loop state
, with color 1, is clearly, by definition, the loop state
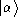 , and we represent it by the diagram
, and we represent it by the diagram
 . The spin network state
. The spin network state
 determined by the graph without nodes
determined by the graph without nodes
 , with color
n
can be obtained as follows. Draw
n
parallel lines along the loop
, with color
n
can be obtained as follows. Draw
n
parallel lines along the loop
 ; cut all lines at an arbitrary point of
; cut all lines at an arbitrary point of
 , and consider the
n
! diagrams obtained by joining the legs after a permutation. The
linear combination of these
n
! diagrams, taken with alternate signs (namely with the sign
determined by the parity of the permutation) is precisely the
state
, and consider the
n
! diagrams obtained by joining the legs after a permutation. The
linear combination of these
n
! diagrams, taken with alternate signs (namely with the sign
determined by the parity of the permutation) is precisely the
state
 . The reason for this key result can be found in the fact that
an irreducible representation of
SU
(2) can be obtained as the totally symmetric tensor product of
the fundamental representation with itself. For details, see [77
. The reason for this key result can be found in the fact that
an irreducible representation of
SU
(2) can be obtained as the totally symmetric tensor product of
the fundamental representation with itself. For details, see [77 ].
].


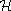 is very useful in concrete calculations. First, associate to a
loop state
is very useful in concrete calculations. First, associate to a
loop state
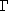 with nodes. Draw
with nodes. Draw
 parallel lines along each link
parallel lines along each link
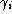 . Join pairwise the end points of these lines at each node (in
an arbitrary manner), in such a way that each line is joined with
a line from a different link (see Figure
. Join pairwise the end points of these lines at each node (in
an arbitrary manner), in such a way that each line is joined with
a line from a different link (see Figure


