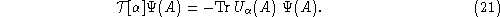
-variables, as linear operators on
. These form a representation of the loop variables Poisson
algebra. The operator
acts diagonally
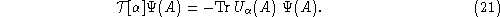
(Recall that products of loop states and spin network states are normalizable states). In diagrammatic notation, the operator simply adds a loop to a (linear combination of) multiloops
Higher order loop operators are expressed in terms of the
elementary ``grasp'' operation. Consider first the operator
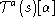, with one hand in the point
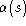. The operator annihilates all loop states that do not cross the
point
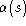. Acting on a loop state
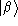, it gives
where we have introduced the elementary length
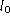by
and
and
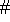are defined in section
6.1
. This action extends by linearity, by continuity and by the
Leibniz rule to products and linear combinations of loop states,
and to the full
. In particular, it is not difficult to compute its action on a
spin network state [77
]. Higher order loop operators act similarly. It is a simple
exercise to verify that these operators provide a representation
of the classical Poisson loop algebra.
All the operators in the theory are then constructed in terms
of these basic loop operators, in the same way in which in
conventional QFT one constructs all operators, including the
hamiltonian, in terms of creation and annihilation operators. The
construction of the composite operators requires the development
of regularization techniques that can be used in the absence of a
background metric. These have been introduced in [196] and developed in [186,
77,
18,
23,
138,
17].
|
Loop Quantum Gravity
Carlo Rovelli http://www.livingreviews.org/lrr-1998-1 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de |
