The kinematics of the theory is well understood, both
physically (quanta of area and volume, polymer-like geometry)
and from the mathematical point of view ( , s-knot states, area and volume operators). The part of the
theory which is not yet fully under control is the dynamics,
which is determined by the hamiltonian constraint. A plausible
candidate for the quantum hamiltonian constraint is the
operator introduced by Thiemann [206,
201,
202]. The commutators of the Thiemann operator with itself and
with the diffeomorphism constraints close, and therefore the
operator defines a complete and consistent quantum theory.
However, doubts have been raised on the physical correctness of
this theory, and some variants of the operator have been
considered.
, s-knot states, area and volume operators). The part of the
theory which is not yet fully under control is the dynamics,
which is determined by the hamiltonian constraint. A plausible
candidate for the quantum hamiltonian constraint is the
operator introduced by Thiemann [206,
201,
202]. The commutators of the Thiemann operator with itself and
with the diffeomorphism constraints close, and therefore the
operator defines a complete and consistent quantum theory.
However, doubts have been raised on the physical correctness of
this theory, and some variants of the operator have been
considered.
The doubts originate from various considerations. First,
Lewandowski, Marolf and others have stressed the fact the
quantum constraint algebra closes, but it is not isomorphic to
the classical constraint algebra of GR [140 ]. Recently, a detailed analysis of this problem has been
completed by Marolf, Lewandowski, Gambini and Pullin [90]. The failure to reproduce the classical constraint algebra
has been disputed, and is not necessarily a problem, since the
only strict requirement on the quantum theory, besides
consistency, is that its
gauge invariant
physical predictions match the ones of classical general
relativity in the appropriate limit. Still, the difference in
the algebras may be seen as circumstantial evidence (not a
proof) for the failure of the classical limit. The issue is
technically delicate and still controversial. I hope I will be
able to say something more definitive in the next update of
this review.
]. Recently, a detailed analysis of this problem has been
completed by Marolf, Lewandowski, Gambini and Pullin [90]. The failure to reproduce the classical constraint algebra
has been disputed, and is not necessarily a problem, since the
only strict requirement on the quantum theory, besides
consistency, is that its
gauge invariant
physical predictions match the ones of classical general
relativity in the appropriate limit. Still, the difference in
the algebras may be seen as circumstantial evidence (not a
proof) for the failure of the classical limit. The issue is
technically delicate and still controversial. I hope I will be
able to say something more definitive in the next update of
this review.
Second, Brügmann [53] and Smolin [192 ] have pointed out a sort of excess ``locality'' in the form of
the operator, which, intuitively, seems in contradiction with
the propagation properties of the Einstein equations. Finally,
by translating the Thiemann operator into a spacetime covariant
four-dimensional formalism, Reisenberger and Rovelli have
noticed a suspicious lack of manifest 4-d covariance in the
action of the operator [160
] have pointed out a sort of excess ``locality'' in the form of
the operator, which, intuitively, seems in contradiction with
the propagation properties of the Einstein equations. Finally,
by translating the Thiemann operator into a spacetime covariant
four-dimensional formalism, Reisenberger and Rovelli have
noticed a suspicious lack of manifest 4-d covariance in the
action of the operator [160 ], a fact pointing again to the possibility of anomalies in the
quantum constraint algebra.
], a fact pointing again to the possibility of anomalies in the
quantum constraint algebra.
Motivated by these doubts, several variants of Thiemann's
operator have been suggested. The original Thiemann's operators
is constructed using the volume operator. There are two
versions of the volume operator in the literature:
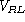 , introduced in [186] and
, introduced in [186] and
 , introduced in [14,
16,
15]. See [139] for a detailed comparison. Originally, Thiemann thought that
using
, introduced in [14,
16,
15]. See [139] for a detailed comparison. Originally, Thiemann thought that
using
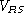 in the hamiltonian constraint would yield difficulties, but it
later became clear that this is not the case [140
in the hamiltonian constraint would yield difficulties, but it
later became clear that this is not the case [140 ]. Both versions of the volume can be used in the definition,
yielding two alternative versions of the hamiltonian [140
]. Both versions of the volume can be used in the definition,
yielding two alternative versions of the hamiltonian [140 ]. Next, in its simplest version the operator is non-symmetric.
Since the classical hamiltonian constraint is real (on
SU
(2) gauge invariant states), one might expect a corresponding
self-adjoint quantum operator.
]. Next, in its simplest version the operator is non-symmetric.
Since the classical hamiltonian constraint is real (on
SU
(2) gauge invariant states), one might expect a corresponding
self-adjoint quantum operator.
 Accordingly, several ways of symmetrizing the operator have
been considered (see a list in [140]). Next, Smolin has considered some ad hoc modifications of
the constraint in [192]. Finally, the spacetime covariant formalism in [160
Accordingly, several ways of symmetrizing the operator have
been considered (see a list in [140]). Next, Smolin has considered some ad hoc modifications of
the constraint in [192]. Finally, the spacetime covariant formalism in [160 ] naturally suggest a ``covariantisation'' of the operator,
described in [160
] naturally suggest a ``covariantisation'' of the operator,
described in [160 ] under the name of ``crossing symmetry''. This
covariantisation amounts to adding to the vertex described in
Figure 3 the vertices, described in Figure 5, which are simply
obtained by re-orienting Figure 3 in spacetime.
] under the name of ``crossing symmetry''. This
covariantisation amounts to adding to the vertex described in
Figure 3 the vertices, described in Figure 5, which are simply
obtained by re-orienting Figure 3 in spacetime.
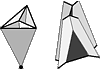
Figure 5: The crossing symmetric vertices.
A full comparative analysis of this various proposals would be of great interest.
Ultimately, the final tests of any proposal for the hamiltonian constraint operator must be consistency and a correct classical limit. Thus, the solution of the hamiltonian constraint puzzle is likely to be subordinate to the solution of the problem of extracting the classical limit (of the dynamics) from the theory.
The basics of the description of matter in the loop
formalism have been established in [150,
151,
133,
26,
207,
200 ]. Work needs to be done in order to develop a full
description of the basic matter couplings. In particular,
there are strong recurring indications that the Planck scale
discreteness naturally cuts the traditional quantum field
infinities off. In particular, in [200], Thiemann argues that the Hamiltonian constraint governing
the coordinate time evolution of the Yang-Mills field is a
well defined operator (I recall that, due to the ultraviolet
divergences, no rigorously well defined hamiltonian operator
for conventional Yang-Mills theory is known in 4 dimensions.)
If these indications are confirmed, the result would be very
remarkable. What is still missing are calculational
techniques that could allow us to connect the well-defined
constraint with finite observables quantities such as
scattering amplitudes.
]. Work needs to be done in order to develop a full
description of the basic matter couplings. In particular,
there are strong recurring indications that the Planck scale
discreteness naturally cuts the traditional quantum field
infinities off. In particular, in [200], Thiemann argues that the Hamiltonian constraint governing
the coordinate time evolution of the Yang-Mills field is a
well defined operator (I recall that, due to the ultraviolet
divergences, no rigorously well defined hamiltonian operator
for conventional Yang-Mills theory is known in 4 dimensions.)
If these indications are confirmed, the result would be very
remarkable. What is still missing are calculational
techniques that could allow us to connect the well-defined
constraint with finite observables quantities such as
scattering amplitudes.
In my view, the development of continuous spacetime
formalisms, [181,
160 ,
33,
144], is one of the most promising areas of development of the
theory, because it might be the key for addressing most of
the open problems. First, a spacetime formalism frees us from
the obscurities of the frozen time formalism, and allows an
intuitive, Feynman-style, description of the dynamics of
quantum spacetime. I think that the classical limit, the
quantum description of black holes, or graviton-graviton
scattering, just to mention a few examples, could be
addressed much more easily in the covariant picture. Second,
it allows the general ideas of Hartle [103] and Isham [119,
120,
123,
122] on the interpretation of generally covariant quantum
theories to be applied in loop quantum gravity. This could
drastically simplify the complications of the canonical way
of dealing with general covariant observables [169,
167]. Third, the spacetime formalism should suggest solutions to
the problem of selecting the correct hamiltonian constraint:
it is usually easier to deal with invariances in the
Lagrangian rather than in the hamiltonian formalisms. The
spacetime formalism is just born, and much has to be done.
See the original papers for suggestions and open
problems.
,
33,
144], is one of the most promising areas of development of the
theory, because it might be the key for addressing most of
the open problems. First, a spacetime formalism frees us from
the obscurities of the frozen time formalism, and allows an
intuitive, Feynman-style, description of the dynamics of
quantum spacetime. I think that the classical limit, the
quantum description of black holes, or graviton-graviton
scattering, just to mention a few examples, could be
addressed much more easily in the covariant picture. Second,
it allows the general ideas of Hartle [103] and Isham [119,
120,
123,
122] on the interpretation of generally covariant quantum
theories to be applied in loop quantum gravity. This could
drastically simplify the complications of the canonical way
of dealing with general covariant observables [169,
167]. Third, the spacetime formalism should suggest solutions to
the problem of selecting the correct hamiltonian constraint:
it is usually easier to deal with invariances in the
Lagrangian rather than in the hamiltonian formalisms. The
spacetime formalism is just born, and much has to be done.
See the original papers for suggestions and open
problems.
The derivation of the Bekenstein-Hawking entropy formula is a major success of loop quantum gravity, but much remains to be understood. A clean derivation from the full quantum theory is not yet available. Such a derivation would require us to understand what, precisely, the event horizon in the quantum theory is. In other words, given a quantum state of the geometry, we should be able to define and ``locate'' its horizon (or whatever structure replaces it in the quantum theory). To do so, we should understand how to effectively deal with the quantum dynamics, how to describe the classical limit (in order to find the quantum states corresponding to classical black hole solutions), as well as how to describe asymptotically flat quantum states.
Besides these formal issues, at the roots of the black
hole entropy puzzle there is a basic physical problem, which,
to my understanding, is still open. The problem is to
understand how we can use basic thermodynamical and
statistical ideas and techniques in a general covariant
context.
 To appreciate the difficulty, notice that statistical
mechanics makes heavy use of the notion of energy (say in the
definition of the canonical or microcanonical ensembles); but
there is no natural local notion of energy associated to a
black hole (or there are too many of such notions). Energy is
an extremely slippery notion in gravity. Thus, how do we
define the statistical ensemble? Put in other words: To
compute the entropy (say in the microcanonical) of a normal
system, we count the states with a given energy. In GR we
should count the states with a given
what
? One may say: black hole states with a given area. But why
so? We do understand why the number of states with given
energy
governs the thermodynamical behavior of normal systems. But
why should the number of states with given
area
govern the thermodynamical behavior of the system, namely
govern its heat exchanges with the exterior? A tentative
physical discussion of this last point can be found in [178].
To appreciate the difficulty, notice that statistical
mechanics makes heavy use of the notion of energy (say in the
definition of the canonical or microcanonical ensembles); but
there is no natural local notion of energy associated to a
black hole (or there are too many of such notions). Energy is
an extremely slippery notion in gravity. Thus, how do we
define the statistical ensemble? Put in other words: To
compute the entropy (say in the microcanonical) of a normal
system, we count the states with a given energy. In GR we
should count the states with a given
what
? One may say: black hole states with a given area. But why
so? We do understand why the number of states with given
energy
governs the thermodynamical behavior of normal systems. But
why should the number of states with given
area
govern the thermodynamical behavior of the system, namely
govern its heat exchanges with the exterior? A tentative
physical discussion of this last point can be found in [178].
Assume we pick a specific hamiltonian constraint. Then we have, in principle, a well defined quantum theory. How do we extract physical information from it? Some physical consequences of the theory, such as the area and volume eigenvalues, or the entropy formula, have been extracted from the theory by various ad hoc methods. But is there a general technique, say corresponding to the traditional QFT perturbation expansion of the S matrix, for describing the full dynamics of the gravitational field? Presumably, such general techniques should involve some kind of expansion, since we could not hope to solve the theory exactly. Attempts to define physical expansions have been initiated in [175] and, in different form, in [160]. Ideally, one would want a general scheme for computing transition amplitudes in some expansion parameter around some state. Computing scattering amplitudes would be of particular interest, in order to make connection with particle physics language and to compare the theory with string predictions.
Finally, to prove that loop quantum gravity is a valuable candidate for describing quantum spacetime, we need to prove that its classical limit is GR (or at least overlaps GR in the regime where GR is well tested). The traditional connection between loop quantum gravity and classical GR is via the notion of weave, a quantum state that ``looks semiclassical'' at distances large compared to the Planck scale. However, the weaves studied so far [23, 99] are 3d weaves, in the sense that they are eigenstates of the three dimensional metric. Such a state corresponds to an eigenstate of the position for a particle. Classical behavior is recovered not by these states but rather by wave packets which have small spread in position as well as in momentum. Similarly, the quantum Minkowski spacetime should have small spread in the three metric as well as in its momentum - as the quantum electromagnetic vacuum has small quantum spread in the electric and magnetic field. To recover classical GR from loop quantum gravity, we must understand such states. Preliminary investigation in this direction can be found in [126, 125], but these papers are now several years old, and they were written before the more recent solidification of the basics of the theory. Another direction consists in the direct study of coherent states in the state space of the theory.



