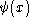on the real line, and express the momentum and the hamiltonian
as differential operators. Denote the eigenstates of the
hamiltonian as
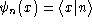. It is well known that the theory can be expressed entirely in
algebraic form in terms of the states
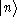. In doing so, all elementary operators are algebraic:
,
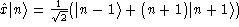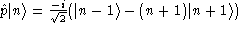. Similarly, in quantum gravity we can directly construct the
quantum theory in the spin-network (or loop) basis, without ever
mentioning functionals of the connections. This representation of
the theory is denoted the ``loop representation''.
A section of the first paper on loop quantum gravity by
Rovelli and Smolin [184
] was devoted to a detailed study of ``transformation theory''
(in the sense of Dirac) on the state space of quantum gravity,
and in particular on the relations between the loop states
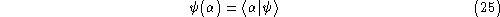
and the states
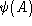giving the amplitude for a connection field configuration
A, and defined by
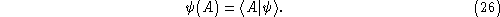
Here
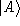are ``eigenstates of the connection operator'', or, more
precisely (since the operator corresponding to the connection is
ill defined in the theory) the generalized states that
satisfy
However, at the time of [184] the lack of a scalar product made transformation theory quite
involved.
On the other hand, the introduction of the scalar product (14
) gives a rigorous meaning to the loop transform. In fact, we can
write, for every spin network
S, and every state
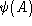
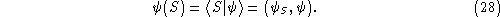
This equation defines a unitary mapping between the two
presentations of
: the ``loop representation'', in which one works in terms of
the basis
; and the ``connection representation'', in which one uses wave
functionals
.
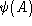The development of the connection representation followed a
winding path through
-algebraic [12] and measure theoretical [14,
16,
15] methods. The work of Ashtekar, Isham, Lewandowski, Marolf,
Mourao and Thiemann has finally put the connection representation
on a firm ground, and, indirectly has much clarified the
mathematics underlying the original loop approach. In the course
of this development, doubts were raised about the precise
relations between the connection and the loop formalisms. Today,
the complete equivalence of these two approaches (always
suspected) has been firmly established. In particular, the work
of Roberto DePietri [76] has proven the unitary equivalence of the two formalisms. For a
recent discussion see also [139].
|
Loop Quantum Gravity
Carlo Rovelli http://www.livingreviews.org/lrr-1998-1 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de |