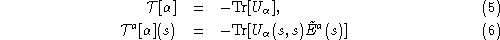
in
M
and the points
we define:
and, in general
where
is the parallel propagator of
along
, defined by
(See [77
] for more details.) These are the loop observables, introduced
in Yang Mills theories in [95,
96], and in gravity in [183,
184].
The loop observables coordinatize the phase space and have a
closed Poisson algebra, denoted by the loop algebra. This algebra
has a remarkable geometrical flavor. For instance, the Poisson
bracket between
and
is non vanishing only if
lies over
; if it does, the result is proportional to the holonomy of the
Wilson loops obtained by joining
and
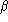at their intersection (by rerouting the 4 legs at the
intersection). More precisely
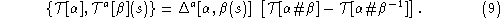
Here
is a vector distribution with support on
and
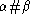is the loop obtained starting at the intersection between
and
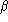, and following first
and then
.
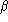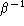is
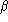with reversed orientation.
A (non-SU(2) gauge invariant) quantity that plays a role in certain aspects of the theory, particularly in the regularization of certain operators, is obtained by integrating the E field over a two dimensional surface S
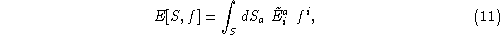
where
f
is a function on the surface
S, taking values in the Lie algebra of
SU
(2). As an alternative to the full loop observables (5,
6
,
7), one can also take the holonomies and
E
[S,
f] as elementary variables [15,
17]; this is more natural to do, for instance, in the C*-algebric
approach [12].
|
Loop Quantum Gravity
Carlo Rovelli http://www.livingreviews.org/lrr-1998-1 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de |
