


The kinematics of a quantum theory is defined by an algebra of
``elementary'' operators (such as
x
and
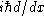 , or creation and annihilation operators) on a Hilbert space
, or creation and annihilation operators) on a Hilbert space
 . The physical interpretation of the theory is based on the
connection between these operators and classical variables, and
on the interpretation of
. The physical interpretation of the theory is based on the
connection between these operators and classical variables, and
on the interpretation of
 as the space of the quantum states. The dynamics is governed by
a hamiltonian, or, as in general relativity, by a set of quantum
constraints, constructed in terms of the elementary operators. To
assure that the quantum Heisenberg equations have the correct
classical limit, the algebra of the elementary operator has to be
isomorphic to the Poisson algebra of the elementary observables.
This yields the heuristic quantization rule: ``promote Poisson
brackets to commutators''. In other words, define the quantum
theory as a linear representation of the Poisson algebra formed
by the elementary observables. For the reasons illustrated in
section
5, the algebra of elementary observables we choose for the
quantization is the loop algebra, defined in section
6.1
. Thus, the kinematic of the quantum theory is defined by a
unitary representation of the loop algebra. Here, I construct
such representation following a simple path.
as the space of the quantum states. The dynamics is governed by
a hamiltonian, or, as in general relativity, by a set of quantum
constraints, constructed in terms of the elementary operators. To
assure that the quantum Heisenberg equations have the correct
classical limit, the algebra of the elementary operator has to be
isomorphic to the Poisson algebra of the elementary observables.
This yields the heuristic quantization rule: ``promote Poisson
brackets to commutators''. In other words, define the quantum
theory as a linear representation of the Poisson algebra formed
by the elementary observables. For the reasons illustrated in
section
5, the algebra of elementary observables we choose for the
quantization is the loop algebra, defined in section
6.1
. Thus, the kinematic of the quantum theory is defined by a
unitary representation of the loop algebra. Here, I construct
such representation following a simple path.
We can start ``à la Schrödinger'' by expressing quantum states
by means of the amplitude of the connection, namely by means of
functionals
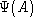 of the (smooth) connection. These functionals form a linear
space, which we promote to a Hilbert space by defining a inner
product. To define the inner product, we choose a particular set
of states, which we denote ``cylindrical states'' and begin by
defining the scalar product between these.
of the (smooth) connection. These functionals form a linear
space, which we promote to a Hilbert space by defining a inner
product. To define the inner product, we choose a particular set
of states, which we denote ``cylindrical states'' and begin by
defining the scalar product between these.
Pick a graph
 , say with
n
links, denoted
, say with
n
links, denoted
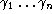 , immersed in the manifold
M
. For technical reasons, we require the links to be analytic. Let
, immersed in the manifold
M
. For technical reasons, we require the links to be analytic. Let
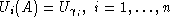 be the parallel transport operator of the connection
A
along
be the parallel transport operator of the connection
A
along
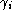 .
.
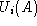 is an element of
SU
(2). Pick a function
is an element of
SU
(2). Pick a function
 on
on
 . The graph
. The graph
 and the function
f
determine a functional of the connection as follows
and the function
f
determine a functional of the connection as follows

(These states are called cylindrical states because they were
introduced in [14 ,
15
,
15 ,
16
,
16 ] as cylindrical functions for the definition of a cylindrical
measure.) Notice that we can always ``enlarge the graph'', in the
sense that if
] as cylindrical functions for the definition of a cylindrical
measure.) Notice that we can always ``enlarge the graph'', in the
sense that if
 is a subgraph of
is a subgraph of
 , we can always write
, we can always write
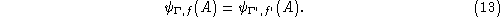
by simply choosing
f
' independent from the
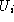 's of the links which are in
's of the links which are in
 but not in
but not in
 . Thus, given any two cylindrical functions, we can always view
them as having the same graph (formed by the union of the two
graphs). Given this observation, we define the scalar product
between any two cylindrical functions [137,
14
. Thus, given any two cylindrical functions, we can always view
them as having the same graph (formed by the union of the two
graphs). Given this observation, we define the scalar product
between any two cylindrical functions [137,
14 ,
15
,
15 ,
16
,
16 ] by
] by
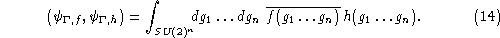
where
dg
is the Haar measure on
SU
(2). This scalar product extends by linearity to finite linear
combinations of cylindrical functions. It is not difficult to
show that (14 ) defines a well defined scalar product on the space of these
linear combinations. Completing the space of these linear
combinations in the Hilbert norm, we obtain a Hilbert space
) defines a well defined scalar product on the space of these
linear combinations. Completing the space of these linear
combinations in the Hilbert norm, we obtain a Hilbert space
 . This is the (unconstrained) quantum state space of loop
gravity.
. This is the (unconstrained) quantum state space of loop
gravity.

 carries a natural unitary representation of the diffeomorphism
group and of the group of the local
SU
(2) transformations, obtained transforming the argument of the
functionals. An important property of the scalar product (14
carries a natural unitary representation of the diffeomorphism
group and of the group of the local
SU
(2) transformations, obtained transforming the argument of the
functionals. An important property of the scalar product (14 ) is that it is invariant under both these transformations.
) is that it is invariant under both these transformations.
 is non-separable. At first sight, this may seem a serious
obstacle to its physical interpretation. But we will see below
that, after factoring away diffeomorphism invariance, we may
obtain a separable Hilbert space (see section
6.8). Also, standard spectral theory holds on
is non-separable. At first sight, this may seem a serious
obstacle to its physical interpretation. But we will see below
that, after factoring away diffeomorphism invariance, we may
obtain a separable Hilbert space (see section
6.8). Also, standard spectral theory holds on
 , and it turns out that using spin networks (discussed below)
one can express
, and it turns out that using spin networks (discussed below)
one can express
 as a direct sum over finite dimensional subspaces which have the
structure of Hilbert spaces of spin systems; this makes practical
calculations very manageable.
as a direct sum over finite dimensional subspaces which have the
structure of Hilbert spaces of spin systems; this makes practical
calculations very manageable.
Finally, we will use a Dirac notation and write
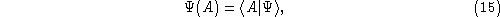
in the same manner in which one may write
 in ordinary quantum mechanics. As in that case, however, we
should remember that
in ordinary quantum mechanics. As in that case, however, we
should remember that
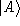 is not a normalizable state.
is not a normalizable state.




|
Loop Quantum Gravity
Carlo Rovelli
http://www.livingreviews.org/lrr-1998-1
© Max-Planck-Gesellschaft. ISSN 1433-8351
Problems/Comments to
livrev@aei-potsdam.mpg.de
|
 of the (smooth) connection. These functionals form a linear
space, which we promote to a Hilbert space by defining a inner
product. To define the inner product, we choose a particular set
of states, which we denote ``cylindrical states'' and begin by
defining the scalar product between these.
of the (smooth) connection. These functionals form a linear
space, which we promote to a Hilbert space by defining a inner
product. To define the inner product, we choose a particular set
of states, which we denote ``cylindrical states'' and begin by
defining the scalar product between these.


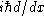 , or creation and annihilation operators) on a Hilbert space
, or creation and annihilation operators) on a Hilbert space
 . The physical interpretation of the theory is based on the
connection between these operators and classical variables, and
on the interpretation of
. The physical interpretation of the theory is based on the
connection between these operators and classical variables, and
on the interpretation of
 , say with
n
links, denoted
, say with
n
links, denoted
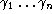 , immersed in the manifold
M
. For technical reasons, we require the links to be analytic. Let
, immersed in the manifold
M
. For technical reasons, we require the links to be analytic. Let
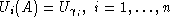 be the parallel transport operator of the connection
A
along
be the parallel transport operator of the connection
A
along
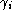 .
.
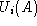 is an element of
SU
(2). Pick a function
is an element of
SU
(2). Pick a function
 on
on
 . The graph
. The graph


 , we can always write
, we can always write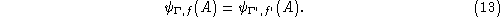
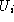 's of the links which are in
's of the links which are in


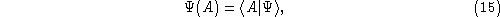
 in ordinary quantum mechanics. As in that case, however, we
should remember that
in ordinary quantum mechanics. As in that case, however, we
should remember that
 is not a normalizable state.
is not a normalizable state.