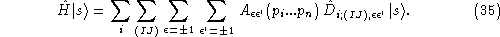



 ,
201
,
201 ,
202
,
202 ] is based on several clever ideas. I will not describe it here.
Rather, I will sketch below the final form of the constraint (for
the Lapse=1 case), following [175
] is based on several clever ideas. I will not describe it here.
Rather, I will sketch below the final form of the constraint (for
the Lapse=1 case), following [175 ].
].
I begin with the Euclidean hamiltonian constraint. We have
Here
i
labels the nodes of the s-knot
s
; (IJ) labels couples of (distinct) links emerging from
i
.
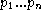 are the colors of the links emerging from
i
.
are the colors of the links emerging from
i
.
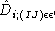 is the operator that acts on an
is the operator that acts on an
 -knot by: (i) creating two additional nodes, one along each of
the two links
I
and
J
; (ii) creating a novel link, colored 1, joining these two nodes,
(iii) assigning the coloring
-knot by: (i) creating two additional nodes, one along each of
the two links
I
and
J
; (ii) creating a novel link, colored 1, joining these two nodes,
(iii) assigning the coloring
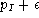 and, respectively,
and, respectively,
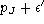 to the links that join the new formed nodes with the node
i
. This is illustrated in Figure 2.
to the links that join the new formed nodes with the node
i
. This is illustrated in Figure 2.

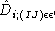 .
.
The coefficients
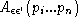 , which are finite, can be expressed explicitly (but in a rather
laborious way) in terms of products of linear combinations of 6-
j
symbols of
SU
(2), following the techniques developed in detail in [77
, which are finite, can be expressed explicitly (but in a rather
laborious way) in terms of products of linear combinations of 6-
j
symbols of
SU
(2), following the techniques developed in detail in [77 ]. Some of these coefficients have been explicitly computed [51
]. Some of these coefficients have been explicitly computed [51 ]. The Lorentzian hamiltonian constraint is given by a similar
expression, but quadratic in the
]. The Lorentzian hamiltonian constraint is given by a similar
expression, but quadratic in the
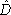 operators.
operators.
The operator defined above is obtained by introducing a
regularized expression for the classical hamiltonian constraint,
written in terms of elementary loop observables, turning these
observables into the corresponding operators and taking the
limit. The construction works rather magically, relying on the
fact, first noticed in [188 ], that certain operator limits
], that certain operator limits
 turn out to be finite on diff invariant states, thanks to the
fact that, for
turn out to be finite on diff invariant states, thanks to the
fact that, for
 and
and
 , sufficiently small,
, sufficiently small,
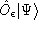 and
and
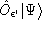 are diffeomorphic equivalent. Thus, here diff invariance plays
again a crucial role in the theory.
are diffeomorphic equivalent. Thus, here diff invariance plays
again a crucial role in the theory.
For a discussion of the problems raised by the Thiemann operator and of the variant proposed, see section 8 .




|
Loop Quantum Gravity
Carlo Rovelli http://www.livingreviews.org/lrr-1998-1 © Max-Planck-Gesellschaft. ISSN 1433-8351 Problems/Comments to livrev@aei-potsdam.mpg.de |