3.2 Spherical coordinates and harmonics
Spherical coordinates (see Figure 19) are well adapted for the study of many problems in numerical
relativity. Those include the numerical modeling of isolated astrophysical single objects, like a neutron star
or a black hole. Indeed, stars’ surfaces have sphere-like shapes and black hole horizons have this topology as
well, which is best described in spherical coordinates (eventually through a mapping, see Section 3.1.1). As
these are isolated systems in general relativity, the exact boundary conditions are imposed at infinity,
requiring a compactification of space, which is here achieved with the compactification of the radial
coordinate  only.
only.
When the numerical grid does not extend to infinity, e.g., when solving for a hyperbolic PDE, the
boundary defined by 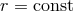 is a smooth surface, on which boundary conditions are much easier to
impose. Finally, spherical harmonics, which are strongly linked with these coordinates, can simplify a lot the
solution of Poisson-like or wave-like equations. On the other hand, there are some technical problems linked
with this set of coordinates, as detailed hereafter, but spectral methods can handle them in a very efficient
way.
is a smooth surface, on which boundary conditions are much easier to
impose. Finally, spherical harmonics, which are strongly linked with these coordinates, can simplify a lot the
solution of Poisson-like or wave-like equations. On the other hand, there are some technical problems linked
with this set of coordinates, as detailed hereafter, but spectral methods can handle them in a very efficient
way.
3.2.1 Coordinate singularities
The transformation from spherical 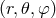 to Cartesian coordinates
to Cartesian coordinates 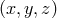 is obtained by
is obtained by
One immediately sees that the origin 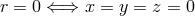 is singular in spherical coordinates
because neither
is singular in spherical coordinates
because neither 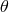 nor
nor  can be uniquely defined. The same happens for the
can be uniquely defined. The same happens for the  -axis, where
-axis, where 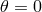 or
or
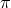 , and
, and 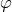 cannot be defined. Among the consequences is the singularity of some usual differential
operators, like, for instance, the Laplace operator
Here, the divisions by
cannot be defined. Among the consequences is the singularity of some usual differential
operators, like, for instance, the Laplace operator
Here, the divisions by  at the center, or by
at the center, or by 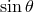 on the
on the  -axis look singular. On the other hand, the
Laplace operator, expressed in Cartesian coordinates, is a perfectly regular one and, if it is
applied to a regular function, should give a well-defined result. The same should be true if
one uses spherical coordinates: the operator (93) applied to a regular function should yield a
regular result. This means that a regular function of spherical coordinates must have a particular
behavior at the origin and on the axis, so that the divisions by
-axis look singular. On the other hand, the
Laplace operator, expressed in Cartesian coordinates, is a perfectly regular one and, if it is
applied to a regular function, should give a well-defined result. The same should be true if
one uses spherical coordinates: the operator (93) applied to a regular function should yield a
regular result. This means that a regular function of spherical coordinates must have a particular
behavior at the origin and on the axis, so that the divisions by  or
or 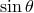 appearing in regular
operators are always well defined. If one considers an analytic function in (regular) Cartesian
coordinates
appearing in regular
operators are always well defined. If one considers an analytic function in (regular) Cartesian
coordinates 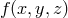 , it can be expanded as a series of powers of
, it can be expanded as a series of powers of 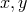 and
and  , near the origin
Placing the coordinate definitions (90)-(92) into this expression gives
and rearranging the terms in
, near the origin
Placing the coordinate definitions (90)-(92) into this expression gives
and rearranging the terms in 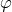 :
With some transformations of trigonometric functions in
:
With some transformations of trigonometric functions in 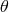 , one can express the angular part in terms of
spherical harmonics
, one can express the angular part in terms of
spherical harmonics 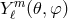 , see Section 3.2.2, with
, see Section 3.2.2, with 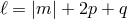 and obtain the two following
regularity conditions, for a given couple
and obtain the two following
regularity conditions, for a given couple  :
:
- near
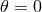 , a regular scalar field is equivalent to
, a regular scalar field is equivalent to  ,
,
- near
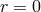 , a regular scalar field is equivalent to
, a regular scalar field is equivalent to 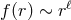 .
.
In addition, the  -dependence translates into a Taylor series near the origin, with the same
parity as
-dependence translates into a Taylor series near the origin, with the same
parity as 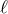 . More details in the case of polar (2D) coordinates are given in Chapter 18 of
Boyd [48].
. More details in the case of polar (2D) coordinates are given in Chapter 18 of
Boyd [48].
If we go back to the evaluation of the Laplace operator (93), it is now clear that the result is always
regular, at least for  and
and 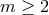 . We detail the cases of
. We detail the cases of 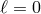 and
and 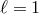 , using the fact that
spherical harmonics are eigenfunctions of the angular part of the Laplace operator (see Equation (103)).
For
, using the fact that
spherical harmonics are eigenfunctions of the angular part of the Laplace operator (see Equation (103)).
For 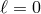 the scalar field
the scalar field 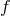 is reduced to a Taylor series of only even powers of
is reduced to a Taylor series of only even powers of  , therefore the
first derivative contains only odd powers and can be safely divided by
, therefore the
first derivative contains only odd powers and can be safely divided by  . Once decomposed
on spherical harmonics, the angular part of the Laplace operator (93) acting on the
. Once decomposed
on spherical harmonics, the angular part of the Laplace operator (93) acting on the  component reads
component reads 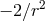 , which is a problem only for the first term of the Taylor expansion.
On the other hand, this term cancels with the
, which is a problem only for the first term of the Taylor expansion.
On the other hand, this term cancels with the 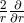 , providing a regular result. This is the
general behavior of many differential operators in spherical coordinates: when applied to a
regular field, the full operator gives a regular result, but single terms of this operator may give
singular results when computed separately, the singularities canceling between two different
terms.
, providing a regular result. This is the
general behavior of many differential operators in spherical coordinates: when applied to a
regular field, the full operator gives a regular result, but single terms of this operator may give
singular results when computed separately, the singularities canceling between two different
terms.
As this may seem an argument against the use of spherical coordinates, let us stress that
spectral methods are very powerful in evaluating such operators, keeping everything finite. As an
example, we use Chebyshev polynomials in 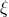 for the expansion of the field
for the expansion of the field  ,
, 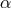 being a positive constant. From the Chebyshev polynomial recurrence relation (46), one has
being a positive constant. From the Chebyshev polynomial recurrence relation (46), one has
which recursively gives the coefficients of
from those of 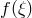 . The computation of this finite part
. The computation of this finite part 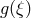 is always a regular and linear operation on
the vector of coefficients. Thus, the singular terms of a regular operator are never computed, but the result
is a good one, as if the cancellation of such terms had occurred. Moreover, from the parity conditions it is
possible to use only even or odd Chebyshev polynomials, which simplifies the expressions and saves
computer time and memory. Of course, relations similar to Equation (97) exist for other families
of orthonormal polynomials, as well as relations that divide by
is always a regular and linear operation on
the vector of coefficients. Thus, the singular terms of a regular operator are never computed, but the result
is a good one, as if the cancellation of such terms had occurred. Moreover, from the parity conditions it is
possible to use only even or odd Chebyshev polynomials, which simplifies the expressions and saves
computer time and memory. Of course, relations similar to Equation (97) exist for other families
of orthonormal polynomials, as well as relations that divide by 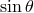 a function developed
on a Fourier basis. The combination of spectral methods and spherical coordinates is thus a
powerful tool for accurately describing regular fields and differential operators inside a sphere [44
a function developed
on a Fourier basis. The combination of spectral methods and spherical coordinates is thus a
powerful tool for accurately describing regular fields and differential operators inside a sphere [44 ].
To our knowledge, this is the first reference showing that it is possible to solve PDEs with
spectral methods inside a sphere, including the three-dimensional coordinate singularity at the
origin.
].
To our knowledge, this is the first reference showing that it is possible to solve PDEs with
spectral methods inside a sphere, including the three-dimensional coordinate singularity at the
origin.
3.2.2 Spherical harmonics
Spherical harmonics are the pure angular functions
where  and
and 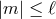 .
. 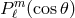 are the associated Legendre functions defined by
for
are the associated Legendre functions defined by
for 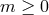 . The relation
gives the associated Legendre functions for negative
. The relation
gives the associated Legendre functions for negative 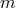 ; note that the normalization factors can vary in
the literature. This family of functions have two very important properties. First, they represent an
orthogonal set of regular functions defined on the sphere; thus, any regular scalar field
; note that the normalization factors can vary in
the literature. This family of functions have two very important properties. First, they represent an
orthogonal set of regular functions defined on the sphere; thus, any regular scalar field  defined on
the sphere can be decomposed into spherical harmonics
Since the harmonics are regular, they automatically take care of the coordinate singularity on the
defined on
the sphere can be decomposed into spherical harmonics
Since the harmonics are regular, they automatically take care of the coordinate singularity on the  -axis.
Then, they are eigenfunctions of the angular part of the Laplace operator (noted here as
-axis.
Then, they are eigenfunctions of the angular part of the Laplace operator (noted here as 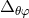 ):
the associated eigenvalues being
):
the associated eigenvalues being 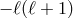 .
.
The first property makes the description of scalar fields on spheres very easy: spherical harmonics are
used as a decomposition basis within spectral methods, for instance in geophysics or meteorology, and by
some groups in numerical relativity [21 , 109
, 109 , 219
, 219 ]. However, they could be more broadly used in numerical
relativity, for example for Cauchy-characteristic evolution or matching [228, 15], where a single coordinate
chart on the sphere might help in matching quantities. They can also help to describe star-like
surfaces being defined by
]. However, they could be more broadly used in numerical
relativity, for example for Cauchy-characteristic evolution or matching [228, 15], where a single coordinate
chart on the sphere might help in matching quantities. They can also help to describe star-like
surfaces being defined by 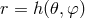 as event or apparent horizons [153, 23
as event or apparent horizons [153, 23 , 2]. The search for
apparent horizons is also made easier: since the function
, 2]. The search for
apparent horizons is also made easier: since the function  verifies a two-dimensional Poisson-like
equation, the linear part can be solved directly, just by dividing by
verifies a two-dimensional Poisson-like
equation, the linear part can be solved directly, just by dividing by  in the coefficient
space.
in the coefficient
space.
The second property makes the Poisson equation,
very easy to solve (see Section 1.3). If the source 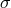 and the unknown
and the unknown 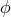 are decomposed into spherical
harmonics, the equation transforms into a set of ordinary differential equations for the coefficients (see
also [109
are decomposed into spherical
harmonics, the equation transforms into a set of ordinary differential equations for the coefficients (see
also [109 ]):
Then, any ODE solver can be used for the radial coordinate: spectral methods, of course, (see Section 2.5),
but others have been used as well (see, e.g., Bartnik et al. [20
]):
Then, any ODE solver can be used for the radial coordinate: spectral methods, of course, (see Section 2.5),
but others have been used as well (see, e.g., Bartnik et al. [20 , 21
, 21 ]). The same technique can be used to
advance in time the wave equation with an implicit scheme and Chebyshev-tau method for the radial
coordinate [44
]). The same technique can be used to
advance in time the wave equation with an implicit scheme and Chebyshev-tau method for the radial
coordinate [44 , 158
, 158 ].
].
The use of spherical-harmonics decomposition can be regarded as a basic spectral method, like Fourier
decomposition. There are, therefore, publicly available “spherical harmonics transforms”, which consist of a
Fourier transform in the 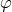 -direction and a successive Fourier and Legendre transform in the
-direction and a successive Fourier and Legendre transform in the
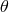 -direction. A rather efficient one is the SpharmonicsKit/S2Kit [152], but writing one’s own functions is
also possible [99
-direction. A rather efficient one is the SpharmonicsKit/S2Kit [152], but writing one’s own functions is
also possible [99 ].
].
3.2.3 Tensor components
All the discussion in Sections 3.2.1 – 3.2.2 has been restricted to scalar fields. For vector, or more generally
tensor fields in three spatial dimensions, a vector basis (triad) must be specified to express the components.
At this point, it is very important to stress that the choice of the basis is independent of the choice of
coordinates. Therefore, the most straightforward and simple choice, even if one is using spherical
coordinates, is the Cartesian triad 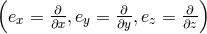 . With this basis, from a numerical
point of view, all tensor components can be regarded as scalars and therefore, a regular tensor
can be defined as a tensor field, whose components with respect to this Cartesian frame are
expandable in powers of
. With this basis, from a numerical
point of view, all tensor components can be regarded as scalars and therefore, a regular tensor
can be defined as a tensor field, whose components with respect to this Cartesian frame are
expandable in powers of 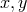 and
and  (as in Bardeen and Piran [19
(as in Bardeen and Piran [19 ]). Manipulations and solutions
of PDEs for such tensor fields in spherical coordinates are generalizations of the techniques
for scalar fields. In particular, when using the multidomain approach with domains having
different shapes and coordinates, it is much easier to match Cartesian components of tensor
fields. Examples of use of Cartesian components of tensor fields in numerical relativity include
the vector Poisson equation [109
]). Manipulations and solutions
of PDEs for such tensor fields in spherical coordinates are generalizations of the techniques
for scalar fields. In particular, when using the multidomain approach with domains having
different shapes and coordinates, it is much easier to match Cartesian components of tensor
fields. Examples of use of Cartesian components of tensor fields in numerical relativity include
the vector Poisson equation [109 ] or, more generally, the solution of elliptic systems arising in
numerical relativity [172
] or, more generally, the solution of elliptic systems arising in
numerical relativity [172 ]. In the case of the evolution of the unconstrained Einstein system, the
use of Cartesian tensor components is the general option, as it is done by the Caltech/Cornell
group [127
]. In the case of the evolution of the unconstrained Einstein system, the
use of Cartesian tensor components is the general option, as it is done by the Caltech/Cornell
group [127 , 189
, 189 ].
].
The use of an orthonormal spherical basis 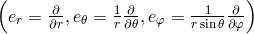 (see. Figure 19) requires
more care. The interested reader can find more details in the work of Bonazzola et al. [44, 37
(see. Figure 19) requires
more care. The interested reader can find more details in the work of Bonazzola et al. [44, 37 ].
Nevertheless, there are systems in general relativity in which spherical components of tensors can be
useful:
].
Nevertheless, there are systems in general relativity in which spherical components of tensors can be
useful:
- When doing excision for the simulation of black holes, the boundary conditions on the excised
sphere for elliptic equations (initial data) may be better formulated in terms of spherical
components for the shift or the three-metric [62
 , 104, 123
, 104, 123 ]. In particular, the component that
is normal to the excised surface is easily identified with the radial component.
]. In particular, the component that
is normal to the excised surface is easily identified with the radial component.
- Still, in the 3+1 approach, the extraction of gravitational radiation in the wave zone is made
easier if the perturbation to the metric is expressed in spherical components, because the
transverse part is then straightforward to obtain [218
 ].
].
Problems arise because of the singular nature of the basis itself, in addition to the spherical coordinate
singularities. The consequences are first that each component is a multivalued function at the origin 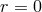 or on the
or on the  -axis, and then that components of a given tensor are not independent from one another,
meaning that one cannot, in general, specify each component independently or set it to zero, keeping the
tensor field regular. As an example, we consider the gradient
-axis, and then that components of a given tensor are not independent from one another,
meaning that one cannot, in general, specify each component independently or set it to zero, keeping the
tensor field regular. As an example, we consider the gradient 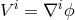 of the scalar field
of the scalar field 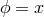 , where
, where
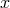 is the usual first Cartesian coordinate field. This gradient expressed in Cartesian components is
a regular vector field
is the usual first Cartesian coordinate field. This gradient expressed in Cartesian components is
a regular vector field 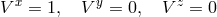 . The spherical components of
. The spherical components of 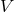 read
read
which are all multidefined at the origin, and the last two on the  -axis. In addition, if
-axis. In addition, if  is set to zero,
one sees that the resulting vector field is no longer regular: for example the square of its norm is
multidefined, which is not a good property for a scalar field. As for the singularities of spherical coordinates,
these difficulties can be properly handled with spectral methods, provided that the decomposition bases are
carefully chosen.
is set to zero,
one sees that the resulting vector field is no longer regular: for example the square of its norm is
multidefined, which is not a good property for a scalar field. As for the singularities of spherical coordinates,
these difficulties can be properly handled with spectral methods, provided that the decomposition bases are
carefully chosen.
The other drawback of spherical coordinates is that the usual partial differential operators mix the
components. This is due to the nonvanishing connection coefficients associated with the spherical flat
metric [37 ]. For example, the vector Laplace operator (
]. For example, the vector Laplace operator (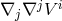 ) reads
) reads
with 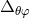 defined in Equation (103). In particular, the
defined in Equation (103). In particular, the  -component (107) of the operator involves the
other two components. This can make the resolution of a vector Poisson equation, which naturally arises in
the initial data problem [61
-component (107) of the operator involves the
other two components. This can make the resolution of a vector Poisson equation, which naturally arises in
the initial data problem [61 ] of numerical relativity, technically more complicated, and the technique using
scalar spherical harmonics (Section 3.2.2) is no longer valid. One possibility can be to use vector, and more
generally tensor [146, 239, 218, 51], spherical harmonics as the decomposition basis. Another technique
might be to build from the spherical components regular scalar fields, which can have a similar
physical relevance to the problem. In the vector case, one can think of the following expressions
where
] of numerical relativity, technically more complicated, and the technique using
scalar spherical harmonics (Section 3.2.2) is no longer valid. One possibility can be to use vector, and more
generally tensor [146, 239, 218, 51], spherical harmonics as the decomposition basis. Another technique
might be to build from the spherical components regular scalar fields, which can have a similar
physical relevance to the problem. In the vector case, one can think of the following expressions
where 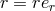 denotes the position vector and
denotes the position vector and 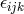 the third-rank fully-antisymmetric tensor. These
scalars are the divergence,
the third-rank fully-antisymmetric tensor. These
scalars are the divergence,  -component and curl of the vector field. The reader can verify that a Poisson
equation for
-component and curl of the vector field. The reader can verify that a Poisson
equation for 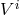 transforms into three equations for these scalars, expandable in terms of scalar spherical
harmonics. The reason that these fields may be more interesting than Cartesian components is that they
can have more physical or geometric meaning.
transforms into three equations for these scalars, expandable in terms of scalar spherical
harmonics. The reason that these fields may be more interesting than Cartesian components is that they
can have more physical or geometric meaning.
![]() is a smooth surface, on which boundary conditions are much easier to
impose. Finally, spherical harmonics, which are strongly linked with these coordinates, can simplify a lot the
solution of Poisson-like or wave-like equations. On the other hand, there are some technical problems linked
with this set of coordinates, as detailed hereafter, but spectral methods can handle them in a very efficient
way.
is a smooth surface, on which boundary conditions are much easier to
impose. Finally, spherical harmonics, which are strongly linked with these coordinates, can simplify a lot the
solution of Poisson-like or wave-like equations. On the other hand, there are some technical problems linked
with this set of coordinates, as detailed hereafter, but spectral methods can handle them in a very efficient
way.
![]() to Cartesian coordinates
to Cartesian coordinates ![]() is obtained by
is obtained by
![]() -dependence translates into a Taylor series near the origin, with the same
parity as
-dependence translates into a Taylor series near the origin, with the same
parity as ![]() . More details in the case of polar (2D) coordinates are given in Chapter 18 of
Boyd [48].
. More details in the case of polar (2D) coordinates are given in Chapter 18 of
Boyd [48].
![]() ), it is now clear that the result is always
regular, at least for
), it is now clear that the result is always
regular, at least for ![]() and
and ![]() . We detail the cases of
. We detail the cases of ![]() and
and ![]() , using the fact that
spherical harmonics are eigenfunctions of the angular part of the Laplace operator (see Equation (103
, using the fact that
spherical harmonics are eigenfunctions of the angular part of the Laplace operator (see Equation (103![]() )).
For
)).
For ![]() the scalar field
the scalar field ![]() is reduced to a Taylor series of only even powers of
is reduced to a Taylor series of only even powers of ![]() , therefore the
first derivative contains only odd powers and can be safely divided by
, therefore the
first derivative contains only odd powers and can be safely divided by ![]() . Once decomposed
on spherical harmonics, the angular part of the Laplace operator (93
. Once decomposed
on spherical harmonics, the angular part of the Laplace operator (93![]() ) acting on the
) acting on the ![]() component reads
component reads ![]() , which is a problem only for the first term of the Taylor expansion.
On the other hand, this term cancels with the
, which is a problem only for the first term of the Taylor expansion.
On the other hand, this term cancels with the ![]() , providing a regular result. This is the
general behavior of many differential operators in spherical coordinates: when applied to a
regular field, the full operator gives a regular result, but single terms of this operator may give
singular results when computed separately, the singularities canceling between two different
terms.
, providing a regular result. This is the
general behavior of many differential operators in spherical coordinates: when applied to a
regular field, the full operator gives a regular result, but single terms of this operator may give
singular results when computed separately, the singularities canceling between two different
terms.
![]() for the expansion of the field
for the expansion of the field ![]() ,
, ![]() being a positive constant. From the Chebyshev polynomial recurrence relation (46
being a positive constant. From the Chebyshev polynomial recurrence relation (46![]() ), one has
), one has
![]() , 109
, 109![]() , 219
, 219![]() ]. However, they could be more broadly used in numerical
relativity, for example for Cauchy-characteristic evolution or matching [228, 15], where a single coordinate
chart on the sphere might help in matching quantities. They can also help to describe star-like
surfaces being defined by
]. However, they could be more broadly used in numerical
relativity, for example for Cauchy-characteristic evolution or matching [228, 15], where a single coordinate
chart on the sphere might help in matching quantities. They can also help to describe star-like
surfaces being defined by ![]() as event or apparent horizons [153, 23
as event or apparent horizons [153, 23![]() , 2]. The search for
apparent horizons is also made easier: since the function
, 2]. The search for
apparent horizons is also made easier: since the function ![]() verifies a two-dimensional Poisson-like
equation, the linear part can be solved directly, just by dividing by
verifies a two-dimensional Poisson-like
equation, the linear part can be solved directly, just by dividing by ![]() in the coefficient
space.
in the coefficient
space.
![]() -direction and a successive Fourier and Legendre transform in the
-direction and a successive Fourier and Legendre transform in the
![]() -direction. A rather efficient one is the SpharmonicsKit/S2Kit [152], but writing one’s own functions is
also possible [99
-direction. A rather efficient one is the SpharmonicsKit/S2Kit [152], but writing one’s own functions is
also possible [99![]() ].
].
![]() . With this basis, from a numerical
point of view, all tensor components can be regarded as scalars and therefore, a regular tensor
can be defined as a tensor field, whose components with respect to this Cartesian frame are
expandable in powers of
. With this basis, from a numerical
point of view, all tensor components can be regarded as scalars and therefore, a regular tensor
can be defined as a tensor field, whose components with respect to this Cartesian frame are
expandable in powers of ![]() and
and ![]() (as in Bardeen and Piran [19
(as in Bardeen and Piran [19![]() ]). Manipulations and solutions
of PDEs for such tensor fields in spherical coordinates are generalizations of the techniques
for scalar fields. In particular, when using the multidomain approach with domains having
different shapes and coordinates, it is much easier to match Cartesian components of tensor
fields. Examples of use of Cartesian components of tensor fields in numerical relativity include
the vector Poisson equation [109
]). Manipulations and solutions
of PDEs for such tensor fields in spherical coordinates are generalizations of the techniques
for scalar fields. In particular, when using the multidomain approach with domains having
different shapes and coordinates, it is much easier to match Cartesian components of tensor
fields. Examples of use of Cartesian components of tensor fields in numerical relativity include
the vector Poisson equation [109![]() ] or, more generally, the solution of elliptic systems arising in
numerical relativity [172
] or, more generally, the solution of elliptic systems arising in
numerical relativity [172![]() ]. In the case of the evolution of the unconstrained Einstein system, the
use of Cartesian tensor components is the general option, as it is done by the Caltech/Cornell
group [127
]. In the case of the evolution of the unconstrained Einstein system, the
use of Cartesian tensor components is the general option, as it is done by the Caltech/Cornell
group [127![]() , 189
, 189![]() ].
].
![]() (see. Figure 19
(see. Figure 19![]() ) requires
more care. The interested reader can find more details in the work of Bonazzola et al. [44, 37
) requires
more care. The interested reader can find more details in the work of Bonazzola et al. [44, 37![]() ].
Nevertheless, there are systems in general relativity in which spherical components of tensors can be
useful:
].
Nevertheless, there are systems in general relativity in which spherical components of tensors can be
useful:
![]() or on the
or on the ![]() -axis, and then that components of a given tensor are not independent from one another,
meaning that one cannot, in general, specify each component independently or set it to zero, keeping the
tensor field regular. As an example, we consider the gradient
-axis, and then that components of a given tensor are not independent from one another,
meaning that one cannot, in general, specify each component independently or set it to zero, keeping the
tensor field regular. As an example, we consider the gradient ![]() of the scalar field
of the scalar field ![]() , where
, where
![]() is the usual first Cartesian coordinate field. This gradient expressed in Cartesian components is
a regular vector field
is the usual first Cartesian coordinate field. This gradient expressed in Cartesian components is
a regular vector field ![]() . The spherical components of
. The spherical components of ![]() read
read
![]() ]. For example, the vector Laplace operator (
]. For example, the vector Laplace operator (![]() ) reads
) reads