1.3 A simple example
Before entering the details of spectral methods in Sections 2, 3 and 4, let us give here their spirit with
the simple example of the Poisson equation in a spherical shell:
where 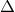 is the Laplace operator (93) expressed in spherical coordinates
is the Laplace operator (93) expressed in spherical coordinates 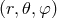 (see also Section 3.2).
We want to solve Equation (7) in the domain where
(see also Section 3.2).
We want to solve Equation (7) in the domain where ![0 < Rmin ≤ r ≤ Rmax, 𝜃 ∈ [0,π ],φ ∈ [0,2 π)](article44x.gif) . This
Poisson equation naturally arises in numerical relativity when, for example, solving for initial conditions or
the Hamiltonian constraint in the 3+1 formalism [97
. This
Poisson equation naturally arises in numerical relativity when, for example, solving for initial conditions or
the Hamiltonian constraint in the 3+1 formalism [97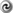 ]: the linear part of these equations can be
cast in form (7), and the nonlinearities put into the source
]: the linear part of these equations can be
cast in form (7), and the nonlinearities put into the source 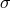 , with an iterative scheme on
, with an iterative scheme on
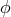 .
.
First, the angular parts of both fields are decomposed into a (finite) set of spherical harmonics 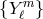 (see Section 3.2.2):
(see Section 3.2.2):
with a similar formula relating 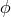 to the radial functions
to the radial functions 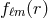 . Because spherical harmonics are
eigenfunctions of the angular part of the Laplace operator, the Poisson equation can be equivalently solved
as a set of ordinary differential equations for each couple
. Because spherical harmonics are
eigenfunctions of the angular part of the Laplace operator, the Poisson equation can be equivalently solved
as a set of ordinary differential equations for each couple 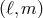 , in terms of the coordinate
, in terms of the coordinate  :
We then map
and decompose each field in a (finite) basis of Chebyshev polynomials
:
We then map
and decompose each field in a (finite) basis of Chebyshev polynomials 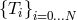 (see Section 2.4.3):
Each function
(see Section 2.4.3):
Each function 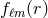 can be regarded as a column-vector
can be regarded as a column-vector 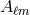 of its
of its 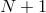 coefficients
coefficients 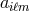 in this
basis; the linear differential operator on the left-hand side of Equation (9) being, thus, a matrix
in this
basis; the linear differential operator on the left-hand side of Equation (9) being, thus, a matrix 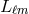 acting on the vector:
with
acting on the vector:
with 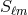 being the vector of the
being the vector of the 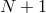 coefficients
coefficients 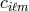 of
of 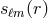 . This matrix can be computed
from the recurrence relations fulfilled by the Chebyshev polynomials and their derivatives (see Section 2.4.3
for details).
. This matrix can be computed
from the recurrence relations fulfilled by the Chebyshev polynomials and their derivatives (see Section 2.4.3
for details).
The matrix 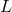 is singular because problem (7) is ill posed. One must indeed specify boundary
conditions at
is singular because problem (7) is ill posed. One must indeed specify boundary
conditions at 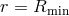 and
and 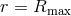 . For simplicity, let us suppose
. For simplicity, let us suppose
To impose these boundary conditions, we adopt the tau methods (see Section 2.5.2): we build the matrix
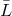 , taking
, taking 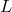 and replacing the last two lines by the boundary conditions, expressed in terms of the
coefficients from the properties of Chebyshev polynomials:
Equations (14) are equivalent to boundary conditions (13), within the considered spectral approximation,
and they represent the last two lines of
and replacing the last two lines by the boundary conditions, expressed in terms of the
coefficients from the properties of Chebyshev polynomials:
Equations (14) are equivalent to boundary conditions (13), within the considered spectral approximation,
and they represent the last two lines of 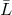 , which can now be inverted and give the coefficients of the
solution
, which can now be inverted and give the coefficients of the
solution 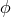 .
.
If one summarizes the steps:
- Setup an adapted grid for the computation of spectral coefficients (e.g., equidistant in the
angular directions and Chebyshev–Gauss–Lobatto collocation points; see Section 2.4.3).
- Get the values of the source
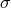 on these grid points.
on these grid points.
- Perform a spherical-harmonics transform (for example, using some available library [152
 ]),
followed by the Chebyshev transform (using a Fast Fourier Transform (FFT), or a
Gauss–Lobatto quadrature) of the source
]),
followed by the Chebyshev transform (using a Fast Fourier Transform (FFT), or a
Gauss–Lobatto quadrature) of the source 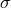 .
.
- For each couple of values
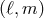 , build the corresponding matrix
, build the corresponding matrix 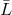 with the boundary
conditions, and invert the system (using any available linear-algebra package) with the
coefficients of
with the boundary
conditions, and invert the system (using any available linear-algebra package) with the
coefficients of 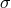 as the right-hand side.
as the right-hand side.
- Perform the inverse spectral transform to get the values of
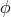 on the grid points from its
coefficients.
on the grid points from its
coefficients.
A numerical implementation of this algorithm has been reported by Grandclément et al. [109 ], who
have observed that the error decayed as
], who
have observed that the error decayed as 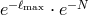 , provided that the source
, provided that the source 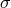 was smooth. Machine
round-off accuracy can be reached with
was smooth. Machine
round-off accuracy can be reached with 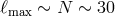 , which makes the matrix inversions of
step 4 very cheap in terms of CPU and the whole method affordable in terms of memory usage.
These are the main advantages of using spectral methods, as shall be shown in the following
sections.
, which makes the matrix inversions of
step 4 very cheap in terms of CPU and the whole method affordable in terms of memory usage.
These are the main advantages of using spectral methods, as shall be shown in the following
sections.
![]() (see Section 3.2.2):
(see Section 3.2.2): ![]() is singular because problem (7
is singular because problem (7![]() ) is ill posed. One must indeed specify boundary
conditions at
) is ill posed. One must indeed specify boundary
conditions at ![]() and
and ![]() . For simplicity, let us suppose
. For simplicity, let us suppose ![]() ], who
have observed that the error decayed as
], who
have observed that the error decayed as ![]() , provided that the source
, provided that the source ![]() was smooth. Machine
round-off accuracy can be reached with
was smooth. Machine
round-off accuracy can be reached with ![]() , which makes the matrix inversions of
step 4 very cheap in terms of CPU and the whole method affordable in terms of memory usage.
These are the main advantages of using spectral methods, as shall be shown in the following
sections.
, which makes the matrix inversions of
step 4 very cheap in terms of CPU and the whole method affordable in terms of memory usage.
These are the main advantages of using spectral methods, as shall be shown in the following
sections.