3 Multidimensional Cases
In principle, the generalization to more than one dimension is rather straightforward if one uses the tensor
product. Let us first take an example, with the spectral representation of a scalar function 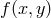 defined
on the square
defined
on the square ![(x,y ) ∈ [− 1,1] × [− 1,1]](article618x.gif) in terms of Chebyshev polynomials. One simply writes
in terms of Chebyshev polynomials. One simply writes
with 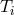 being the Chebyshev polynomial of degree
being the Chebyshev polynomial of degree 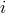 . The partial differential operators can also be
generalized as being linear operators acting on the space
. The partial differential operators can also be
generalized as being linear operators acting on the space 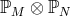 . Simple linear partial differential
equations (PDE) can be solved by one of the methods presented in Section 2.5 (Galerkin, tau or
collocation), on this
. Simple linear partial differential
equations (PDE) can be solved by one of the methods presented in Section 2.5 (Galerkin, tau or
collocation), on this 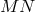 -dimensional space. The development (88) can of course be generalized to any
dimension. Some special PDE and spectral basis examples, where the differential equation decouples for
some of the coordinates, will be given in Section 3.2.
-dimensional space. The development (88) can of course be generalized to any
dimension. Some special PDE and spectral basis examples, where the differential equation decouples for
some of the coordinates, will be given in Section 3.2.
![]() defined
on the square
defined
on the square ![]() in terms of Chebyshev polynomials. One simply writes
in terms of Chebyshev polynomials. One simply writes