Going further: High-order time schemes

4.5 Going further: High-order time schemes

When using spectral methods in time-dependent problems, it is sometimes frustrating to have such accurate numerical techniques for the evaluation of spatial derivatives and the integration of elliptic PDEs, while the time derivatives and hyperbolic PDEs do not benefit from spectral convergence. Some tentative studies are being undertaken in order to represent the time interval by spectral methods as well [113 ]. In their spherically-symmetric study of the wave equation in Minkowski spacetime, Hennig and Ansorg have applied spectral methods to both spatial and time coordinates. Moreover, they have used a conformal compactification of Minkowski spacetime, making the wave equation singular at null infinity. They have obtained nicely accurate and spectrally convergent solutions, even to a nonlinear wave equation. If these techniques can be applied in general three-dimensional simulations, it would really be a great improvement.

Nevertheless, there are other, more sophisticated and accurate time-integration techniques that are currently being investigated for several stiff PDEs [124 ], including Korteweg–de Vries and nonlinear Schrödinger equations [129 ]. Many such PDEs share the properties of being stiff (very different time scales/characteristic frequencies) and combining low-order nonlinear terms with higher-order linear terms. Einstein’s evolution equations can also be written in such a way [37 ]. Let us consider a PDE

using the notation of Section 4.1.1 and 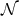$𝒩$ as a nonlinear spatial operator. Following the same notation and within spectral approximation, one recovers

We will now describe five methods of solving this type of ODE (see also [124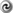

]):

Implicit-explicit techniques use an explicit multistep scheme to advance the nonlinear part 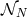$𝒩N$ , and an implicit one for the linear part.
Split-step techniques are effective when the equation splits into two equations, which can be directly integrated (see [129 ] for examples with the nonlinear Schrödinger and Korteweg–de Vries equations).
Integrating factor is a change of variable that allows for the exact solution of the linear part

and explicit multistep method for the integration of the new nonlinear part
Sliders can be seen as an extension of the implicit-explicit method described above. In addition to splitting the problem into a linear and nonlinear part, the linear part itself is split into two or three regions (in Fourier space), depending on the wavenumber. Then, different numerical schemes are used for different groups of wavenumbers: implicit schemes for high wavenumbers and explicit high-order methods for low wavenumbers. This method is restricted to Fourier spectral techniques in space.
Exponential time-differencing techniques have been known for some time in computational electrodynamics. These methods are similar to the integrating factor technique, but one considers the exact equation over one timestep

Various orders for these schemes come from the approximation order of the integral. For example Kassam and Trefethen [124 ] consider a fourth-order Runge–Kutta type approximation to this integral, where the difficulty comes from the accurate computation of functions, that suffer from cancellation errors.