4.1 Time discretization
There have been very few theoretical developments in spectral time discretization, with the exception of
Ierley et al. [121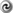 ], where the authors have applied spectral methods in time to the study of the
Korteweg–de Vries and Burger equations, using Fourier series in space and Chebyshev polynomials for the
time coordinates. Ierley et al. [121] observe a timestepping restriction: they have to employ multidomain
and patching techniques (see Section 2.6) for the time interval, with the size of each subdomain being
roughly given by the Courant–Friedrichs–Lewy (CFL) condition. Therefore, the most common
approach for time representation are finite-difference techniques, which allow for the use of many
well-established time-marching schemes, and the method of lines (for other methods, including fractional
stepping, see Fornberg [79]). Let us write the general form of a first-order-in-time linear PDE:
where
], where the authors have applied spectral methods in time to the study of the
Korteweg–de Vries and Burger equations, using Fourier series in space and Chebyshev polynomials for the
time coordinates. Ierley et al. [121] observe a timestepping restriction: they have to employ multidomain
and patching techniques (see Section 2.6) for the time interval, with the size of each subdomain being
roughly given by the Courant–Friedrichs–Lewy (CFL) condition. Therefore, the most common
approach for time representation are finite-difference techniques, which allow for the use of many
well-established time-marching schemes, and the method of lines (for other methods, including fractional
stepping, see Fornberg [79]). Let us write the general form of a first-order-in-time linear PDE:
where 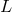 is a linear operator containing only derivatives with respect to the spatial coordinate
is a linear operator containing only derivatives with respect to the spatial coordinate 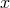 . For
every value of time
. For
every value of time 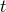 , the spectral approximation
, the spectral approximation 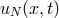 is a function of only one spatial
dimension belonging to some finite-dimensional subspace of the suitable Hilbert space
is a function of only one spatial
dimension belonging to some finite-dimensional subspace of the suitable Hilbert space 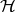 , with
the given
, with
the given 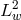 spatial norm, associated for example with the scalar product and the weight
spatial norm, associated for example with the scalar product and the weight
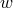 introduced in Section 2.3.1. Formally, the solution of Equation (116) can be written as:
In practice, to integrate time-dependent problems one can use spectral methods to calculate spatial
derivatives and standard finite-difference schemes to advance in time.
introduced in Section 2.3.1. Formally, the solution of Equation (116) can be written as:
In practice, to integrate time-dependent problems one can use spectral methods to calculate spatial
derivatives and standard finite-difference schemes to advance in time.
4.1.1 Method of lines
At every instant 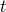 , one can represent the function
, one can represent the function 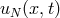 by a finite set
by a finite set 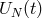 , composed of its
time-dependent spectral coefficients or its values at the collocation points. We denote
, composed of its
time-dependent spectral coefficients or its values at the collocation points. We denote 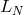 the spectral
approximation to the operator
the spectral
approximation to the operator 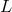 , together with the boundary conditions, if the tau or collocation method
is used.
, together with the boundary conditions, if the tau or collocation method
is used. 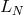 is, therefore, represented as an
is, therefore, represented as an 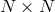 matrix. This is the method of lines, which allows one
to reduce a PDE to an ODE, after discretization in all but one dimensions. The advantage is that many
ODE integration schemes are known (Runge–Kutta, symplectic integrators, ...) and can be
used here. We shall suppose an equally-spaced grid in time, with the timestep noted
matrix. This is the method of lines, which allows one
to reduce a PDE to an ODE, after discretization in all but one dimensions. The advantage is that many
ODE integration schemes are known (Runge–Kutta, symplectic integrators, ...) and can be
used here. We shall suppose an equally-spaced grid in time, with the timestep noted 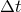 and
and
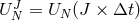 .
.
In order to step from 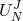 to
to 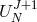 , one has essentially two possibilities: explicit and implicit
schemes. In an explicit scheme, the action of the spatial operator
, one has essentially two possibilities: explicit and implicit
schemes. In an explicit scheme, the action of the spatial operator 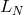 on
on 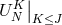 must be computed to
explicitly get the new values of the field (either spatial spectral coefficients or values at collocation points).
A simple example is the forward Euler method:
must be computed to
explicitly get the new values of the field (either spatial spectral coefficients or values at collocation points).
A simple example is the forward Euler method:
which is first order and for which, as for any explicit schemes, the timestep is limited by the CFL condition.
The imposition of boundary conditions is discussed in Section 4.2. With an implicit scheme one must solve
for a boundary value problem in term of 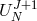 at each timestep: it can be performed in the same way as
for the solution of the elliptic equation (62) presented in Section 2.5.2. The simplest example is the
backward Euler method:
which can be re-written as an equation for the unknown
at each timestep: it can be performed in the same way as
for the solution of the elliptic equation (62) presented in Section 2.5.2. The simplest example is the
backward Euler method:
which can be re-written as an equation for the unknown 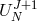 :
:
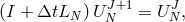 where
where 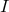 is the identity operator. Both schemes have different stability properties, which can be
analyzed as follows. Assuming that
is the identity operator. Both schemes have different stability properties, which can be
analyzed as follows. Assuming that 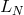 can be diagonalized in the sense of the definition given in
(4.1.3), the stability study can be reduced to the study of the collection of scalar ODE problems
where
can be diagonalized in the sense of the definition given in
(4.1.3), the stability study can be reduced to the study of the collection of scalar ODE problems
where 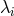 is any of the eigenvalues of
is any of the eigenvalues of 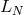 in the sense of Equation (124).
in the sense of Equation (124).
4.1.2 Stability
The basic definition of stability for an ODE integration scheme is that, if the timestep is lower than some
threshold, then 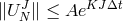 , with constants
, with constants 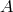 and
and 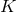 independent of the timestep. This is
perhaps not the most appropriate definition, since in practice one often deals with bounded functions and
an exponential growth in time would not be acceptable. Therefore, an integration scheme is said to be
absolutely stable (or asymptotically stable), if
independent of the timestep. This is
perhaps not the most appropriate definition, since in practice one often deals with bounded functions and
an exponential growth in time would not be acceptable. Therefore, an integration scheme is said to be
absolutely stable (or asymptotically stable), if 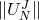 remains bounded,
remains bounded, 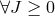 . This property depends
on a particular value of the product
. This property depends
on a particular value of the product 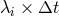 . For each time integration scheme, the region of absolute
stability is the set of the complex plane containing all the
. For each time integration scheme, the region of absolute
stability is the set of the complex plane containing all the 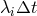 for which the scheme is absolutely
stable.
for which the scheme is absolutely
stable.
Finally, a scheme is said to be 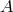 -stable if its region of absolute stability contains the half complex
plane of numbers with negative real part. It is clear that no explicit scheme can be
-stable if its region of absolute stability contains the half complex
plane of numbers with negative real part. It is clear that no explicit scheme can be 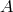 -stable due to the
CFL condition. It has been shown by Dahlquist [66
-stable due to the
CFL condition. It has been shown by Dahlquist [66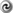 ] that there is no linear multistep method of order
higher than two, which is
] that there is no linear multistep method of order
higher than two, which is 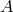 -stable. Thus implicit methods are also limited in timestep size, if more than
second-order accurate. In addition, Dahlquist [66
-stable. Thus implicit methods are also limited in timestep size, if more than
second-order accurate. In addition, Dahlquist [66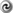 ] shows that the most accurate second-order
] shows that the most accurate second-order 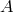 -stable
scheme is the trapezoidal one (also called Crank–Nicolson, or second-order Adams–Moulton scheme)
-stable
scheme is the trapezoidal one (also called Crank–Nicolson, or second-order Adams–Moulton scheme)
Figures 20 and 21 display the absolute stability regions for the Adams–Bashforth and Runge–Kutta
families of explicit schemes (see, for instance, [56 ]). For a given type of spatial linear operator, the
requirement on the timestep usually comes from the largest (in modulus) eigenvalue of the operator. For
example, in the case of the advection equation on
]). For a given type of spatial linear operator, the
requirement on the timestep usually comes from the largest (in modulus) eigenvalue of the operator. For
example, in the case of the advection equation on ![[− 1,1]](article832x.gif) , with a Dirichlet boundary condition,
, with a Dirichlet boundary condition,
and using a Chebyshev-tau method, one can see that the largest eigenvalue of 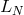 grows in modulus as
grows in modulus as
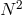 . Therefore, for any of the schemes considered in Figures 20 and 21, the timestep has a restriction of
the type
which can be related to the usual CFL condition by the fact that the minimal distance between two points
of a (
. Therefore, for any of the schemes considered in Figures 20 and 21, the timestep has a restriction of
the type
which can be related to the usual CFL condition by the fact that the minimal distance between two points
of a (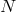 -point) Chebyshev grid decreases like
-point) Chebyshev grid decreases like 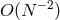 . Due to the above mentioned Second
Dahlquist barrier [66], implicit time marching schemes of order higher than two also have such a
limitation.
. Due to the above mentioned Second
Dahlquist barrier [66], implicit time marching schemes of order higher than two also have such a
limitation.
4.1.3 Spectrum of simple spatial operators
An important issue in determining the absolute stability of a time-marching scheme for the solution of a
given PDE is the computation of the spectrum 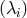 of the discretized spatial operator
of the discretized spatial operator 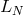 (120). As a
matter of fact, these eigenvalues are those of the matrix representation of
(120). As a
matter of fact, these eigenvalues are those of the matrix representation of 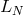 , together with the
necessary boundary conditions for the problem to be well posed (e.g.,
, together with the
necessary boundary conditions for the problem to be well posed (e.g., 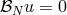 ). If one denotes
). If one denotes
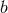 the number of such boundary conditions, each eigenvalue
the number of such boundary conditions, each eigenvalue 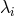 (here, in the case of the
tau method) is defined by the existence of a non-null set of coefficients
(here, in the case of the
tau method) is defined by the existence of a non-null set of coefficients 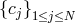 such that
such that
As an example, let us consider the case of the advection equation (first-order spatial derivative) with a
Dirichlet boundary condition, solved with the Chebyshev-tau method (122). Because of the definition of
the problem (124), there are  “eigenvalues”, which can be computed, after a small
transformation, using any standard linear algebra package. For instance, it is possible, making use
of the boundary condition, to express the last coefficient as a combination of the other ones
“eigenvalues”, which can be computed, after a small
transformation, using any standard linear algebra package. For instance, it is possible, making use
of the boundary condition, to express the last coefficient as a combination of the other ones
One is thus left with the usual eigenvalue problem for an 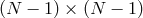 matrix. Results are displayed
in Figure 22 for three values of
matrix. Results are displayed
in Figure 22 for three values of 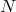 . Real parts are all negative: the eigenvalue that is not displayed lies on
the negative part of the real axis and is much larger in modulus (it is growing as
. Real parts are all negative: the eigenvalue that is not displayed lies on
the negative part of the real axis and is much larger in modulus (it is growing as 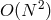 ) than the
) than the
 others.
others.
This way of determining the spectrum can be, of course, generalized to any linear spatial operator, for
any spectral basis, as well as to the collocation and Galerkin methods. Intuitively from CFL-type
limitations, one can see that in the case of the heat equation (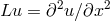 ), explicit time-integration
schemes (or any scheme that is not
), explicit time-integration
schemes (or any scheme that is not 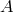 -stable) will have a severe timestep limitation of the type
-stable) will have a severe timestep limitation of the type
for both a Chebyshev or Legendre decomposition basis. Finally, one can decompose a higher-order-in-time
PDE into a first-order system and then use one of the above proposed schemes. In the particular case of the
wave equation,
it is possible to write a second-order Crank-Nicolson scheme directly [158 ]:
Since this scheme is
]:
Since this scheme is 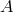 -stable, there is no limitation on the timestep
-stable, there is no limitation on the timestep 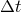 , but for explicit or
higher-order schemes this limitation would be
, but for explicit or
higher-order schemes this limitation would be 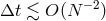 , as for the advection equation. The
solution of such an implicit scheme is obtained as that of a boundary value problem at each
timestep.
, as for the advection equation. The
solution of such an implicit scheme is obtained as that of a boundary value problem at each
timestep.
4.1.4 Semi-implicit schemes
It is sometimes possible to use a combination of implicit and explicit schemes to loosen a timestep
restriction of the type (123). Let us consider, as an example, the advection equation with nonconstant
velocity on ![[− 1,1]](article863x.gif) ,
,
with the relevant boundary conditions, which shall in general depend on the sign of 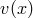 . If, on the one
hand, the stability condition for explicit time schemes (123) is too strong, and on the other hand an
implicit scheme is too lengthy to implement or to use (because of the nonconstant coefficient
. If, on the one
hand, the stability condition for explicit time schemes (123) is too strong, and on the other hand an
implicit scheme is too lengthy to implement or to use (because of the nonconstant coefficient
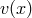 ), then it is interesting to consider the semi-implicit two-step method (see also [94
), then it is interesting to consider the semi-implicit two-step method (see also [94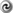 ])
where
])
where 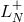 and
and 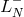 are respectively the spectral approximations to the constant operators
are respectively the spectral approximations to the constant operators 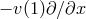 and
and 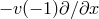 , together with the relevant boundary conditions (if any). This scheme is absolutely
stable if
With this type of scheme, the propagation of the wave at the boundary of the interval is treated implicitly,
whereas the scheme is still explicit in the interior. The implementation of the implicit part, for which one
needs to solve a boundary-value problem, is much easier than for the initial operator (129)
because of the presence of only constant-coefficient operators. This technique is quite helpful in
the case of more severe timestep restrictions (126), for example for a variable coefficient heat
equation.
, together with the relevant boundary conditions (if any). This scheme is absolutely
stable if
With this type of scheme, the propagation of the wave at the boundary of the interval is treated implicitly,
whereas the scheme is still explicit in the interior. The implementation of the implicit part, for which one
needs to solve a boundary-value problem, is much easier than for the initial operator (129)
because of the presence of only constant-coefficient operators. This technique is quite helpful in
the case of more severe timestep restrictions (126), for example for a variable coefficient heat
equation.
![]() , one can represent the function
, one can represent the function ![]() by a finite set
by a finite set ![]() , composed of its
time-dependent spectral coefficients or its values at the collocation points. We denote
, composed of its
time-dependent spectral coefficients or its values at the collocation points. We denote ![]() the spectral
approximation to the operator
the spectral
approximation to the operator ![]() , together with the boundary conditions, if the tau or collocation method
is used.
, together with the boundary conditions, if the tau or collocation method
is used. ![]() is, therefore, represented as an
is, therefore, represented as an ![]() matrix. This is the method of lines, which allows one
to reduce a PDE to an ODE, after discretization in all but one dimensions. The advantage is that many
ODE integration schemes are known (Runge–Kutta, symplectic integrators, ...) and can be
used here. We shall suppose an equally-spaced grid in time, with the timestep noted
matrix. This is the method of lines, which allows one
to reduce a PDE to an ODE, after discretization in all but one dimensions. The advantage is that many
ODE integration schemes are known (Runge–Kutta, symplectic integrators, ...) and can be
used here. We shall suppose an equally-spaced grid in time, with the timestep noted ![]() and
and
![]() .
.
![]() to
to ![]() , one has essentially two possibilities: explicit and implicit
schemes. In an explicit scheme, the action of the spatial operator
, one has essentially two possibilities: explicit and implicit
schemes. In an explicit scheme, the action of the spatial operator ![]() on
on ![]() must be computed to
explicitly get the new values of the field (either spatial spectral coefficients or values at collocation points).
A simple example is the forward Euler method:
must be computed to
explicitly get the new values of the field (either spatial spectral coefficients or values at collocation points).
A simple example is the forward Euler method: ![]() , with constants
, with constants ![]() and
and ![]() independent of the timestep. This is
perhaps not the most appropriate definition, since in practice one often deals with bounded functions and
an exponential growth in time would not be acceptable. Therefore, an integration scheme is said to be
absolutely stable (or asymptotically stable), if
independent of the timestep. This is
perhaps not the most appropriate definition, since in practice one often deals with bounded functions and
an exponential growth in time would not be acceptable. Therefore, an integration scheme is said to be
absolutely stable (or asymptotically stable), if ![]() remains bounded,
remains bounded, ![]() . This property depends
on a particular value of the product
. This property depends
on a particular value of the product ![]() . For each time integration scheme, the region of absolute
stability is the set of the complex plane containing all the
. For each time integration scheme, the region of absolute
stability is the set of the complex plane containing all the ![]() for which the scheme is absolutely
stable.
for which the scheme is absolutely
stable.
![]() -stable if its region of absolute stability contains the half complex
plane of numbers with negative real part. It is clear that no explicit scheme can be
-stable if its region of absolute stability contains the half complex
plane of numbers with negative real part. It is clear that no explicit scheme can be ![]() -stable due to the
CFL condition. It has been shown by Dahlquist [66
-stable due to the
CFL condition. It has been shown by Dahlquist [66![]() ] that there is no linear multistep method of order
higher than two, which is
] that there is no linear multistep method of order
higher than two, which is ![]() -stable. Thus implicit methods are also limited in timestep size, if more than
second-order accurate. In addition, Dahlquist [66
-stable. Thus implicit methods are also limited in timestep size, if more than
second-order accurate. In addition, Dahlquist [66![]() ] shows that the most accurate second-order
] shows that the most accurate second-order ![]() -stable
scheme is the trapezoidal one (also called Crank–Nicolson, or second-order Adams–Moulton scheme)
-stable
scheme is the trapezoidal one (also called Crank–Nicolson, or second-order Adams–Moulton scheme)
![]() and 21
and 21![]() display the absolute stability regions for the Adams–Bashforth and Runge–Kutta
families of explicit schemes (see, for instance, [56
display the absolute stability regions for the Adams–Bashforth and Runge–Kutta
families of explicit schemes (see, for instance, [56![]() ]). For a given type of spatial linear operator, the
requirement on the timestep usually comes from the largest (in modulus) eigenvalue of the operator. For
example, in the case of the advection equation on
]). For a given type of spatial linear operator, the
requirement on the timestep usually comes from the largest (in modulus) eigenvalue of the operator. For
example, in the case of the advection equation on ![]() , with a Dirichlet boundary condition,
, with a Dirichlet boundary condition,
![]() of the discretized spatial operator
of the discretized spatial operator ![]() (120
(120![]() ). As a
matter of fact, these eigenvalues are those of the matrix representation of
). As a
matter of fact, these eigenvalues are those of the matrix representation of ![]() , together with the
necessary boundary conditions for the problem to be well posed (e.g.,
, together with the
necessary boundary conditions for the problem to be well posed (e.g., ![]() ). If one denotes
). If one denotes
![]() the number of such boundary conditions, each eigenvalue
the number of such boundary conditions, each eigenvalue ![]() (here, in the case of the
tau method) is defined by the existence of a non-null set of coefficients
(here, in the case of the
tau method) is defined by the existence of a non-null set of coefficients ![]() such that
such that
![]() ). Because of the definition of
the problem (124
). Because of the definition of
the problem (124![]() ), there are
), there are ![]() “eigenvalues”, which can be computed, after a small
transformation, using any standard linear algebra package. For instance, it is possible, making use
of the boundary condition, to express the last coefficient as a combination of the other ones
“eigenvalues”, which can be computed, after a small
transformation, using any standard linear algebra package. For instance, it is possible, making use
of the boundary condition, to express the last coefficient as a combination of the other ones
![]() ), explicit time-integration
schemes (or any scheme that is not
), explicit time-integration
schemes (or any scheme that is not ![]() -stable) will have a severe timestep limitation of the type
-stable) will have a severe timestep limitation of the type
![]() ). Let us consider, as an example, the advection equation with nonconstant
velocity on
). Let us consider, as an example, the advection equation with nonconstant
velocity on ![]() ,
,