Polynomial interpolation

2.3 Polynomial interpolation

2.3.1 Orthogonal polynomials

Spectral methods are often based on the notion of orthogonal polynomials. In order to define orthogonality, one must define the scalar product of two functions on an interval $[− 1,1]$ . Let us consider a positive function $w$ of $[− 1,1]$ called the measure. The scalar product of $f$ and $g$ with respect to this measure is defined as:

A basis of $Pℕ$ is then a set of $N + 1$ polynomials ${pn}n=0...N$ . $pn$ is of degree $n$ and the polynomials are orthogonal: $(pi,pj)w = 0$ for $i ⁄= j$ .

The projection $PN f$ of a function $f$ on this basis is then

where the coefficients of the projection are given by

The difference between $f$ and its projection goes to zero when $N$ increases:

Figure 6

shows the function $3 3 f = cos (πx ∕2) + (x + 1) ∕8$ and its projection on Chebyshev polynomials (see Section 2.4.3) for $N = 4$ and $N = 8$ , illustrating the rapid convergence of $PN f$ to $f$ .

Figure 6: Function $f = cos3(πx ∕2) + (x + 1 )3 ∕8$ (black curve) and its projection on Chebyshev polynomials (red curve), for $N = 4$ (left panel) and $N = 8$ (right panel).

At first sight, the projection seems to be an interesting means of numerically representing a function. However, in practice this is not the case. Indeed, to determine the projection of a function, one needs to compute the integrals (30 ), which requires the evaluation of $f$ at a great number of points, making the whole numerical scheme impractical.

2.3.2 Gaussian quadratures

The main theorem of Gaussian quadratures (see for instance [57 ]) states that, given a measure $w$ , there exist $N + 1$ positive real numbers $wn$ and $N + 1$ real numbers $xn ∈ [− 1,1 ]$ such that:

The $wn$ are called the weights and the $xn$ are the collocation points. The integer $δ$ can take several values depending on the exact quadrature considered:

Gauss quadrature: $δ = 1$ .
Gauss–Radau: $δ = 0$ and $x0 = − 1$ .
Gauss–Lobatto: $δ = − 1$ and $x0 = − 1, xN = 1$ .

Gauss quadrature is the best choice because it applies to polynomials of higher degree but Gauss–Lobatto quadrature is often more useful for numerical purposes because the outermost collocation points coincide with the boundaries of the interval, making it easier to impose matching or boundary conditions. More detailed results and demonstrations about those quadratures can be found for instance in [57 ].

2.3.3 Spectral interpolation

As already stated in 2.3.1, the main drawback of projecting a function in terms of orthogonal polynomials comes from the difficulty to compute the integrals (30 ). The idea of spectral methods is to approximate the coefficients of the projection by making use of Gaussian quadratures. By doing so, one can define the interpolant of a function $f$ by

where

The $&tidle;fn$ exactly coincides with the coefficients $ˆfn$ , if the Gaussian quadrature is applicable for computing Equation (30

), that is, for all $f ∈ ℙN+ δ$ . So, in general, $IN f ⁄= PN f$ and the difference between the two is called the aliasing error. The advantage of using $f&tidle;n$ is that they are computed by estimating $f$ at the $N + 1$ collocation points only.

One can show that $INf$ and $f$ coincide at the collocation points: $INf (xi) = f (xi)$ so that $IN$ interpolates $f$ on the grid, whose nodes are the collocation points. Figure 7 shows the function $3 3 f = cos (π∕2) + (x + 1) ∕8$ and its spectral interpolation using Chebyshev polynomials, for $N = 4$ and $N = 6$ .

Figure 7: Function $f = cos3(πx ∕2) + (x + 1)3∕8$ (black curve) and its interpolant $IN f$ on Chebyshev polynomials (red curve), for $N = 4$ (left panel) and $N = 6$ (right panel). The collocation points are denoted by the blue circles and correspond to Gauss–Lobatto quadrature.

2.3.4 Two equivalent descriptions

The description of a function $f$ in terms of its spectral interpolation can be given in two different, but equivalent spaces:

in the configuration space, if the function is described by its value at the $N + 1$ collocation points $f (xi)$ ;
in the coefficient space, if one works with the $N + 1$ coefficients $f&tidle; i$ .

There is a bijection between both spaces and the following relations enable us to go from one to the other:

the coefficients can be computed from the values of $f (xi)$ using Equation (34 );
the values at the collocation points are expressed in terms of the coefficients by making use of the definition of the interpolant (33 ):

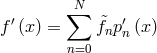Depending on the operation one has to perform on a given function, it may be more clever to work in one space or the other. For instance, the square root of a function is very easily given in the collocation space by $∘ ------ f (xi)$ , whereas the derivative can be computed in the coefficient space if, and this is generally the case, the derivatives of the basis polynomials are known, by $N∑ f ′(x ) = f&tidle;np ′n(x) n=0$ .