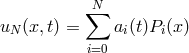4.3 Discretization in space: stability and convergence
After dealing with temporal discretization, we now turn to another fundamental question of numerical
analysis of initial value problems, which is to find conditions under which the discrete (spatial)
approximation 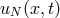 converges to the right solution
converges to the right solution 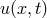 of the PDE (116) as
of the PDE (116) as 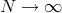 and
and
![t ∈ [0, T]](article932x.gif) . The time derivative term is treated formally, as one would treat a source term on the
right-hand side, that we do not consider here, for better clarity.
. The time derivative term is treated formally, as one would treat a source term on the
right-hand side, that we do not consider here, for better clarity.
A given spatial scheme of solving the PDE is said to be convergent if any numerical approximation
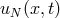 , obtained through this scheme, to the solution
, obtained through this scheme, to the solution 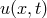
Two more concepts are helpful in the convergence analysis of numerical schemes:
- consistency: an approximation to the PDE (116) is consistent if
 both
both
- stability: with the formal notations of Equation (117), an approximation to the PDE (116) is stable if
where
 is independent of
is independent of 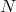 and bounded for
and bounded for ![t ∈ [0,T ]](article941x.gif) .
.
4.3.1 Lax–Richtmyer theorem
The direct proof of convergence of a given scheme is usually very difficult to obtain. Therefore, a natural
approach is to use the Lax–Richtmyer equivalence theorem: “a consistent approximation to a well-posed
linear problem is stable if and only if it is convergent”. Thus, the study of convergence of discrete
approximations can be reduced to the study of their stability, assuming they are consistent. Hereafter, we
sketch out the proof of this equivalence theorem.
The time-evolution PDE (116) is approximated by
To show that stability implies convergence, we subtract it from the exact solution (116)
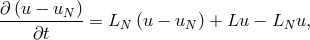 and
obtain, after integration, (the dependence on the space coordinate
and
obtain, after integration, (the dependence on the space coordinate 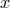 is skipped)
Using the stability property (143), the norm (
is skipped)
Using the stability property (143), the norm (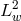 ) of this equation implies
Since the spatial approximation scheme is consistent and
) of this equation implies
Since the spatial approximation scheme is consistent and 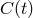 is a bounded function independent of
is a bounded function independent of
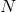 , for a given
, for a given ![t ∈ [0, T]](article950x.gif) the left-hand side goes to zero as
the left-hand side goes to zero as 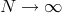 , which proves the
convergence.
, which proves the
convergence.
Conversely, to show that convergence implies stability, we use the triangle inequality to
get
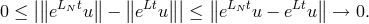 From
the well-posedness
From
the well-posedness 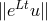 is bounded and therefore
is bounded and therefore 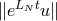 is bounded as well, independent of
is bounded as well, independent of
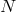 .
.
The simplest stability criterion is the von Neumann stability condition: if we define the adjoint 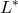 of
the operator
of
the operator 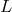 , using the inner product, with weight
, using the inner product, with weight 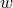 of the Hilbert space
of the Hilbert space
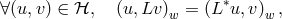 then
the matrix representation
then
the matrix representation 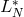 of
of 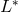 is also the adjoint of the matrix representation of
is also the adjoint of the matrix representation of 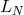 . The
operator
. The
operator 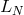 is said to be normal if it commutes with its adjoint
is said to be normal if it commutes with its adjoint 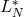 . The von Neumann stability
condition states that, for normal operators, if there exists a constant
. The von Neumann stability
condition states that, for normal operators, if there exists a constant 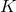 independent of
independent of 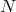 , such that
with
, such that
with 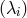 being the eigenvalues of the matrix
being the eigenvalues of the matrix 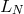 , then the scheme is stable. This condition provides an
operational technique for checking the stability of normal approximations. Unfortunately, spectral
approximations using orthogonal polynomials have, in general, strongly non-normal matrices
, then the scheme is stable. This condition provides an
operational technique for checking the stability of normal approximations. Unfortunately, spectral
approximations using orthogonal polynomials have, in general, strongly non-normal matrices 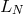 and
therefore, the von Neumann condition cannot be applied. Some exceptions include Fourier-based spectral
approximations for periodic problems.
and
therefore, the von Neumann condition cannot be applied. Some exceptions include Fourier-based spectral
approximations for periodic problems.
4.3.2 Energy estimates for stability
The most straightforward technique for establishing the stability of spectral schemes is the
energy method: it is based on choosing the approximate solution itself as a test function in the
evaluation of residual (60). However, this technique only provides a sufficient condition and, in
particular, crude energy estimates indicating that a spectral scheme might be unstable can be very
misleading for non-normal evolution operators (see the example in Section 8 of Gottlieb and
Orszag [94]).
Some sufficient conditions on the spatial operator 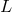 and its approximation
and its approximation 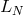 are used in the
literature to obtain energy estimates and stability criteria, including:
are used in the
literature to obtain energy estimates and stability criteria, including:
- If the operator
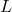 is semibounded:
where
is semibounded:
where 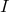 is the identity operator.
is the identity operator.
- In the parabolic case, if
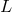 satisfies the coercivity condition (see also Chapter 6.5 of
Canuto et al. [57
satisfies the coercivity condition (see also Chapter 6.5 of
Canuto et al. [57 ]):
and the continuity condition:
]):
and the continuity condition:
- In the hyperbolic case, if there exists a constant
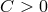 such that
and if the operator verifies the negativity condition:
such that
and if the operator verifies the negativity condition:
As an illustration, we now consider a Galerkin method applied to the solution of Equation (116), in
which the operator 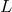 is semibounded, following the definition (148). The discrete solution
is semibounded, following the definition (148). The discrete solution
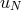 is such that the residual (60) estimated on the approximate solution
is such that the residual (60) estimated on the approximate solution 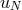 itself verifies
itself verifies
Separating the time derivative and the spatial operator:
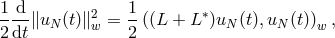 which shows that the “energy”
grows at most exponentially with time. Since
which shows that the “energy”
grows at most exponentially with time. Since 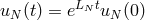 for any
for any 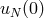 , we obtain
which gives stability and therefore convergence, provided that the approximation is consistent (thanks to
the Lax–Richtmyer theorem).
, we obtain
which gives stability and therefore convergence, provided that the approximation is consistent (thanks to
the Lax–Richtmyer theorem).
4.3.3 Examples: heat equation and advection equation
4.3.3.1 Heat equation
We first study the linear heat equation
with homogeneous Dirichlet boundary conditions
and initial condition
In the semidiscrete approach, the Chebyshev collocation method for this problem (see Section 2.5.3) can
de devised as follows: the spectral solution 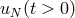 is a polynomial of degree
is a polynomial of degree 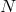 on the
interval
on the
interval ![[− 1,1]](article996x.gif) , vanishing at the endpoints. On the other Chebyshev–Gauss–Lobatto collocation
points
, vanishing at the endpoints. On the other Chebyshev–Gauss–Lobatto collocation
points 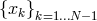 (see Section 2.4.3),
(see Section 2.4.3), 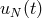 is defined through the collocation equations
which are time ODEs (discussed in Section 4.1) with the initial conditions
is defined through the collocation equations
which are time ODEs (discussed in Section 4.1) with the initial conditions
We will now discuss the stability of such a scheme, with the computation of the energy bound to the
solution. Multiplying the 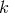 -th equation of the system (159) by
-th equation of the system (159) by 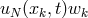 , where
, where 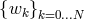 are the
discrete weights of the Chebyshev–Gauss–Lobatto quadrature (Section 2.4.3), and summing over
are the
discrete weights of the Chebyshev–Gauss–Lobatto quadrature (Section 2.4.3), and summing over 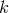 , one
gets:
, one
gets:
Boundary points (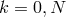 ) have been included in the sum since
) have been included in the sum since 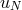 is zero there due to boundary
conditions. The product
is zero there due to boundary
conditions. The product 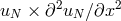 is a polynomial of degree
is a polynomial of degree 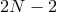 , so the quadrature formula is
exact
and integrating by parts twice, one gets the relation
By the properties of the Chebyshev weight
it is possible to show that
and thus that
Therefore, integrating relation (161) over the time interval
, so the quadrature formula is
exact
and integrating by parts twice, one gets the relation
By the properties of the Chebyshev weight
it is possible to show that
and thus that
Therefore, integrating relation (161) over the time interval ![[0,t]](article1015x.gif) , one obtains
The left-hand side represents the discrete norm of
, one obtains
The left-hand side represents the discrete norm of 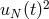 , but since this is a polynomial of degree
, but since this is a polynomial of degree
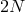 , one cannot apply the Gauss–Lobatto rule. Nevertheless, it has been shown (see, e.g.,
Section 5.3 of Canuto et al. [57
, one cannot apply the Gauss–Lobatto rule. Nevertheless, it has been shown (see, e.g.,
Section 5.3 of Canuto et al. [57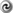 ]) that discrete and
]) that discrete and 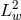 -norms are uniformly equivalent, therefore:
which proves the stability of the Chebyshev collocation method for the heat equation. Convergence can
again be deduced from the Lax–Richtmyer theorem, but a detailed analysis cf. Section 6.5.1 of
Canuto et al. [57
-norms are uniformly equivalent, therefore:
which proves the stability of the Chebyshev collocation method for the heat equation. Convergence can
again be deduced from the Lax–Richtmyer theorem, but a detailed analysis cf. Section 6.5.1 of
Canuto et al. [57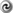 ]) shows that the numerical solution obtained by the method described here converges to
the true solution and one can obtain the convergence rate. If the solution
]) shows that the numerical solution obtained by the method described here converges to
the true solution and one can obtain the convergence rate. If the solution 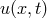 is
is 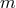 -times
differentiable with respect to the spatial coordinate
-times
differentiable with respect to the spatial coordinate 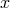 (see Section 2.4.4) the energy norm of the error
decays as
(see Section 2.4.4) the energy norm of the error
decays as 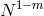 . In particular, if the solution is
. In particular, if the solution is 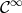 , the error decays faster than any power of
, the error decays faster than any power of
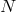 .
.
4.3.3.2 Advection equation
We now study the Legendre-tau approximation to the simple advection equation
with homogeneous Dirichlet boundary condition
and initial condition
If we seek the solution as the truncated Legendre series:
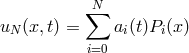 by
the tau method, then
by
the tau method, then 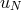 satisfies the equation:
Equating coefficients of
satisfies the equation:
Equating coefficients of 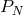 on both sides of (172), we get
on both sides of (172), we get
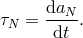 Applying the
Applying the 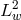 scalar product with
scalar product with 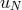 to both sides of Equation (172), we obtain
to both sides of Equation (172), we obtain
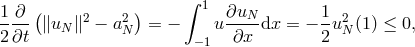 which implies the following inequality:
Finally,
which implies the following inequality:
Finally, 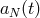 is bounded because it is determined in terms of
is bounded because it is determined in terms of 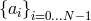 from the boundary
condition (170), and thus, stability is proved. In the same way as before, for the heat equation, it is possible
to derive a bound for the error
from the boundary
condition (170), and thus, stability is proved. In the same way as before, for the heat equation, it is possible
to derive a bound for the error 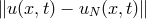 , if the solution
, if the solution 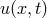 is
is 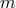 -times differentiable
with respect to the spatial coordinate
-times differentiable
with respect to the spatial coordinate 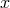 ; the energy norm of the error decays like
; the energy norm of the error decays like 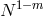 (see also
Section 6.5.2 of Canuto et al. [57]). In particular, if the solution is
(see also
Section 6.5.2 of Canuto et al. [57]). In particular, if the solution is 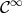 , the error decays faster than any
power of
, the error decays faster than any
power of 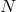 .
.
![]() , obtained through this scheme, to the solution
, obtained through this scheme, to the solution ![]()
![]() ) is approximated by
) is approximated by ![]() of
the operator
of
the operator ![]() , using the inner product, with weight
, using the inner product, with weight ![]() of the Hilbert space
of the Hilbert space
![]() ). However, this technique only provides a sufficient condition and, in
particular, crude energy estimates indicating that a spectral scheme might be unstable can be very
misleading for non-normal evolution operators (see the example in Section 8 of Gottlieb and
Orszag [94]).
). However, this technique only provides a sufficient condition and, in
particular, crude energy estimates indicating that a spectral scheme might be unstable can be very
misleading for non-normal evolution operators (see the example in Section 8 of Gottlieb and
Orszag [94]).
![]() and its approximation
and its approximation ![]() are used in the
literature to obtain energy estimates and stability criteria, including:
are used in the
literature to obtain energy estimates and stability criteria, including:
![]() ), in
which the operator
), in
which the operator ![]() is semibounded, following the definition (148
is semibounded, following the definition (148![]() ). The discrete solution
). The discrete solution
![]() is such that the residual (60
is such that the residual (60![]() ) estimated on the approximate solution
) estimated on the approximate solution ![]() itself verifies
itself verifies
![]() -th equation of the system (159
-th equation of the system (159![]() ) by
) by ![]() , where
, where ![]() are the
discrete weights of the Chebyshev–Gauss–Lobatto quadrature (Section 2.4.3), and summing over
are the
discrete weights of the Chebyshev–Gauss–Lobatto quadrature (Section 2.4.3), and summing over ![]() , one
gets:
, one
gets: