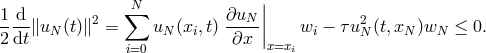4.2 Imposition of boundary conditions
The time-dependent PDE (116) can be written as a system of ODEs in time either for the
time-dependent spectral coefficients 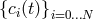 of the unknown function
of the unknown function 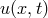 (Galerkin or tau
methods), or for the time-dependent values at collocation points
(Galerkin or tau
methods), or for the time-dependent values at collocation points 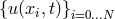 (collocation method).
Implicit time-marching schemes (like the backward Euler scheme (119)) are technically very similar to a
succession of boundary-value problems, as for elliptic equations or Equation (62) described in Section 2.5.
The coefficients (or the values at collocation points) are determined at each new timestep by inversion of
the matrix of type
(collocation method).
Implicit time-marching schemes (like the backward Euler scheme (119)) are technically very similar to a
succession of boundary-value problems, as for elliptic equations or Equation (62) described in Section 2.5.
The coefficients (or the values at collocation points) are determined at each new timestep by inversion of
the matrix of type 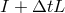 or its higher-order generalization. To represent a well-posed problem, this
matrix needs, in general, the incorporation of boundary conditions, for tau and collocation
methods. Galerkin methods are not so useful if the boundary conditions are time dependent:
this would require the construction of a new Galerkin basis at each new timestep, which is
too complicated and/or time consuming. We shall therefore discuss in the following sections
the imposition of boundary conditions for explicit time schemes, with the tau or collocation
methods.
or its higher-order generalization. To represent a well-posed problem, this
matrix needs, in general, the incorporation of boundary conditions, for tau and collocation
methods. Galerkin methods are not so useful if the boundary conditions are time dependent:
this would require the construction of a new Galerkin basis at each new timestep, which is
too complicated and/or time consuming. We shall therefore discuss in the following sections
the imposition of boundary conditions for explicit time schemes, with the tau or collocation
methods.
4.2.1 Strong enforcement
The standard technique is to enforce the boundary conditions exactly, i.e. up to machine precision. Let us
suppose here that the time-dependent PDE (116), which we want to solve, is well posed with boundary
condition
where 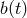 is a given function. We give here some examples, with the forward Euler scheme (118) for time
discretization.
is a given function. We give here some examples, with the forward Euler scheme (118) for time
discretization.
In the collocation method, the values of the approximate solution at (Gauss–Lobatto type)
collocation points 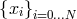 are determined by a system of equations:
are determined by a system of equations:
where the value at the boundary 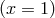 is directly set to be the boundary condition.
is directly set to be the boundary condition.
In the tau method, the vector 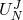 is composed of the
is composed of the 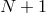 coefficients
coefficients 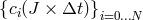 at
the
at
the 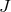 -th timestep. If we denote by
-th timestep. If we denote by 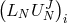 the
the 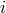 -th coefficient of
-th coefficient of 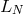 applied to
applied to 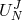 , then the
vector of coefficients
, then the
vector of coefficients 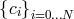 is advanced in time through the system:
is advanced in time through the system:
the last equality ensures the boundary condition in the coefficient space.
4.2.2 Penalty approach
As shown in the previous examples, the standard technique consists of neglecting the solution to the PDE
for one degree of freedom, in configuration or coefficient space, and using this degree of freedom in order to
impose the boundary condition. However, it is interesting to try and impose a linear combination of both
the PDE and the boundary condition on this last degree of freedom, as is shown by the next simple
example. We consider the simple (time-independent) integration over the interval ![x ∈ [− 1, 1]](article892x.gif) :
:
where 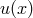 is the unknown function. Using a standard Chebyshev relation (161)collocation method (see
Section 2.5.3), we look for an approximate solution
is the unknown function. Using a standard Chebyshev relation (161)collocation method (see
Section 2.5.3), we look for an approximate solution  as a polynomial of degree
as a polynomial of degree 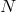 verifying
where
verifying
where  are the Chebyshev–Gauss–Lobatto collocation points.
are the Chebyshev–Gauss–Lobatto collocation points.
We now adopt another procedure that takes into account the differential equation at the
boundary as well as the boundary condition, with 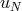 verifying (remember that
verifying (remember that 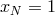 ):
):
where 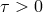 is a constant; one notices when taking the limit
is a constant; one notices when taking the limit 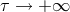 , that both systems become
equivalent. The discrepancy between the numerical and analytical solutions is displayed in Figure 23, as a
function of that parameter
, that both systems become
equivalent. The discrepancy between the numerical and analytical solutions is displayed in Figure 23, as a
function of that parameter 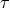 , when using
, when using 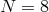 . It is clear from that figure that there exists a finite
value of
. It is clear from that figure that there exists a finite
value of 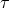 (
(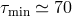 ) for which the error is minimal and, in particular, lower than the error obtained
by the standard technique. Numerical evidence indicates that
) for which the error is minimal and, in particular, lower than the error obtained
by the standard technique. Numerical evidence indicates that 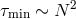 . This is a simple example of
weakly imposed boundary conditions, with a penalty term added to the system. The idea of imposing
boundary conditions up to the order of the numerical scheme was first proposed by Funaro and
Gottlieb [85] and can be efficiently used for time-dependent problems, as illustrated by the following
example. For a more detailed description, we refer the interested reader to the review article by
Hesthaven [115
. This is a simple example of
weakly imposed boundary conditions, with a penalty term added to the system. The idea of imposing
boundary conditions up to the order of the numerical scheme was first proposed by Funaro and
Gottlieb [85] and can be efficiently used for time-dependent problems, as illustrated by the following
example. For a more detailed description, we refer the interested reader to the review article by
Hesthaven [115 ].
].
Let us consider the linear advection equation
where 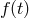 is a given function. We look for a Legendre collocation method to obtain a solution, and define
the polynomial
is a given function. We look for a Legendre collocation method to obtain a solution, and define
the polynomial 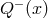 , which vanishes on the Legendre–Gauss–Lobatto grid points, except at the
boundary
, which vanishes on the Legendre–Gauss–Lobatto grid points, except at the
boundary 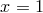 :
:
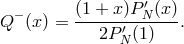 Thus,
the Legendre collocation penalty method uniquely defines a polynomial
Thus,
the Legendre collocation penalty method uniquely defines a polynomial 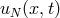 through its values at
Legendre–Gauss–Lobatto collocation points
through its values at
Legendre–Gauss–Lobatto collocation points 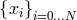 where
where 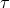 is a free parameter as in Equation (136). For all the grid points, except the boundary one, this is
the same as the standard Legendre collocation method (
is a free parameter as in Equation (136). For all the grid points, except the boundary one, this is
the same as the standard Legendre collocation method ( ). At the
boundary point
). At the
boundary point 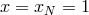 , one has a linear combination of the advection equation and the
boundary condition. Contrary to the case of the simple integration (136), the parameter
, one has a linear combination of the advection equation and the
boundary condition. Contrary to the case of the simple integration (136), the parameter 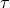 here
cannot be too small: in the limit
here
cannot be too small: in the limit 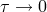 , the problem is ill posed and the numerical solution
diverges. On the other hand, we still recover the standard (strong) imposition of boundary
conditions when
, the problem is ill posed and the numerical solution
diverges. On the other hand, we still recover the standard (strong) imposition of boundary
conditions when 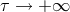 . With the requirement that the approximation be asymptotically stable,
we get for the discrete energy estimate (see the details of this technique in Section 4.3.2) the
requirement
. With the requirement that the approximation be asymptotically stable,
we get for the discrete energy estimate (see the details of this technique in Section 4.3.2) the
requirement
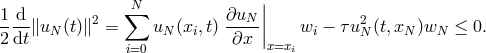 Using
the property of Gauss–Lobatto quadrature rule (with the Legendre–Gauss–Lobatto weights
Using
the property of Gauss–Lobatto quadrature rule (with the Legendre–Gauss–Lobatto weights 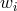 ), and after
an integration by parts, the stability is obtained if
It is also possible to treat more complex boundary conditions, as described in Hesthaven and Gottlieb [116]
in the case of Robin-type boundary conditions (see Section 2.5.1 for a definition). Specific conditions for the
penalty coefficient
), and after
an integration by parts, the stability is obtained if
It is also possible to treat more complex boundary conditions, as described in Hesthaven and Gottlieb [116]
in the case of Robin-type boundary conditions (see Section 2.5.1 for a definition). Specific conditions for the
penalty coefficient 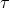 are derived, but the technique is the same: for each boundary, a penalty term is
added, which is proportional to the error on the boundary condition at the considered time. Thus, nonlinear
boundary operators can also be incorporated easily (see, e.g., the case of the Burgers equation in [115]).
The generalization to multidomain solutions is straightforward: each domain is considered as an isolated
one, which requires boundary conditions at every timestep. The condition is imposed through
the penalty term containing the difference between the junction conditions. This approach
has very strong links with the variational method presented in Section 2.6.5 in the case of
time-independent problems. A more detailed discussion of the weak imposition of boundary
conditions is given in Canuto et al. (Section 3.7 of [57
are derived, but the technique is the same: for each boundary, a penalty term is
added, which is proportional to the error on the boundary condition at the considered time. Thus, nonlinear
boundary operators can also be incorporated easily (see, e.g., the case of the Burgers equation in [115]).
The generalization to multidomain solutions is straightforward: each domain is considered as an isolated
one, which requires boundary conditions at every timestep. The condition is imposed through
the penalty term containing the difference between the junction conditions. This approach
has very strong links with the variational method presented in Section 2.6.5 in the case of
time-independent problems. A more detailed discussion of the weak imposition of boundary
conditions is given in Canuto et al. (Section 3.7 of [57 ] and Section 5.3 of [58] for multidomain
methods).
] and Section 5.3 of [58] for multidomain
methods).
![]() ), which we want to solve, is well posed with boundary
condition
), which we want to solve, is well posed with boundary
condition ![]() are determined by a system of equations:
are determined by a system of equations: ![]() is composed of the
is composed of the ![]() coefficients
coefficients ![]() at
the
at
the ![]() -th timestep. If we denote by
-th timestep. If we denote by ![]() the
the ![]() -th coefficient of
-th coefficient of ![]() applied to
applied to ![]() , then the
vector of coefficients
, then the
vector of coefficients ![]() is advanced in time through the system:
is advanced in time through the system: ![]() :
:

![]() verifying (remember that
verifying (remember that ![]() ):
):