4.2 Near zone contribution
We shall evaluate the near zone contribution as follows. First, we make a retarded expansion of
Equation (75) and change the integral region to a 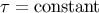 spatial hypersurface,
Note that the above integral depends on the arbitrary length
spatial hypersurface,
Note that the above integral depends on the arbitrary length 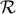 in general. The cancellation between the
in general. The cancellation between the
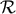 dependent terms in the far zone contribution and those in the near zone contribution was shown
by [129
dependent terms in the far zone contribution and those in the near zone contribution was shown
by [129 ] through all the post-Newtonian order. In the following, we shall omit the terms which have
negative powers of
] through all the post-Newtonian order. In the following, we shall omit the terms which have
negative powers of 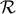 (
(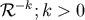 ). In other words, we simply let
). In other words, we simply let  whenever it gives a
convergent result. On the other hand, we shall retain terms having positive powers of
whenever it gives a
convergent result. On the other hand, we shall retain terms having positive powers of 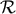 (
(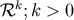 ), and logarithmic terms (
), and logarithmic terms (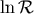 ) to confirm that the final result, in the end of
calculation, is independent of
) to confirm that the final result, in the end of
calculation, is independent of 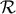 (and for logarithmic terms to keep the arguments of logarithm
non-dimensional).
(and for logarithmic terms to keep the arguments of logarithm
non-dimensional).
Second we split the integral into two parts: a contribution from the body zone 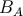 , and from
elsewhere,
, and from
elsewhere, 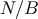 . Schematically we evaluate the following two types of integrals (we omit indices of the
field),
. Schematically we evaluate the following two types of integrals (we omit indices of the
field),
where 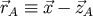 . We shall deal with these two contributions successively.
. We shall deal with these two contributions successively.
4.2.1 Body zone contribution
As for the body zone contribution, we make a multipole expansion using the scaling of the integrand,
i.e. 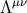 in the body zone. For example, the
in the body zone. For example, the 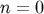 part in Equation (76),
part in Equation (76),  , gives
, gives
Here the operator 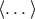 denotes a symmetric and tracefree (STF) operation on the indices in the brackets.
See [129
denotes a symmetric and tracefree (STF) operation on the indices in the brackets.
See [129 , 150, 165
, 150, 165 ] for some useful formulas of STF tensors. Also we define
] for some useful formulas of STF tensors. Also we define  . To derive the
3 PN equations of motion,
. To derive the
3 PN equations of motion, 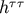 up to
up to 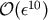 and
and 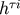 as well as
as well as 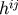 up to
up to 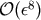 are
required.
are
required.
In the above equations we define the multipole moments as
where we introduced a collective multi-index  and
and 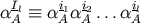 . Then
. Then 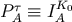 ,
, 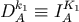 ,
and
,
and 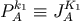 . We simply call
. We simply call 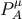 the four-momentum of the star
the four-momentum of the star 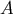 ,
, 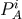 the momentum, and
the momentum, and 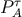 the
energy.
Also we call
the
energy.
Also we call 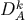 the dipole moment of the star
the dipole moment of the star 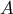 , and
, and 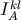 the quadrupole moment of the star
the quadrupole moment of the star
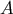 .
.
Then we transform these moments into more convenient forms. By the conservation law (67), we have
where 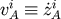 , an overdot denotes a time derivative with respect to
, an overdot denotes a time derivative with respect to 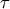 , and
, and 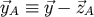 . Using these
equations and noticing that the body zone remains unchanged (in the near zone coordinates),
i.e.
. Using these
equations and noticing that the body zone remains unchanged (in the near zone coordinates),
i.e.  , we have
where
and
The operators
, we have
where
and
The operators ![[ ]](article385x.gif) and
and 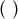 attached to the indices denote anti-symmetrization and symmetrization.
attached to the indices denote anti-symmetrization and symmetrization.
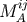 is the spin of the star
is the spin of the star  and Equation (86) is the momentum-velocity relation. Thus our
momentum-velocity relation is a direct analog of the Newtonian momentum-velocity relation (see
Section 3.4). In general, we have
and
where
and Equation (86) is the momentum-velocity relation. Thus our
momentum-velocity relation is a direct analog of the Newtonian momentum-velocity relation (see
Section 3.4). In general, we have
and
where 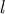 is the number of indices in the multi-index
is the number of indices in the multi-index  .
.
Now, from the above equations, especially Equation (88), we find that the body zone contributions,
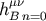 , are of order
, are of order 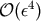 . Note that if we can not or do not assume the (nearly) stationarity of the
initial data for the stars, then, instead of Equation (88) we have
. Note that if we can not or do not assume the (nearly) stationarity of the
initial data for the stars, then, instead of Equation (88) we have
where we used the dynamical time 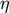 (see Section 3.3). In this case the lowest order metric differs from
the Newtonian form. From our (almost) stationarity assumption the remaining motion inside a star, apart
from the spinning motion, is caused only by the tidal effect by the companion star and from Equation (88);
it appears at 3 PN order [81
(see Section 3.3). In this case the lowest order metric differs from
the Newtonian form. From our (almost) stationarity assumption the remaining motion inside a star, apart
from the spinning motion, is caused only by the tidal effect by the companion star and from Equation (88);
it appears at 3 PN order [81 ].
].
To obtain the lowest order 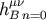 , we have to evaluate the surface integrals
, we have to evaluate the surface integrals 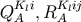 . Generally, in
. Generally, in
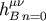 the moments
the moments 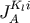 and
and 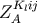 appear formally at the order
appear formally at the order 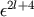 and
and 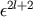 . Thus
. Thus 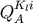 and
and 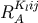 appear as
appear as
where we omitted irrelevant terms and numerical coefficients. Thus one may expect that 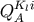 and
and 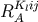 appear at the order
appear at the order 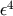 for any
for any 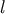 and we have to calculate an infinite number of moments. In fact, this is
not the case and it was shown in [91
and we have to calculate an infinite number of moments. In fact, this is
not the case and it was shown in [91 ] that only
] that only 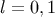 terms of
terms of 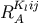 contribute to the 3 PN
equations of motion. The important thing here is that
contribute to the 3 PN
equations of motion. The important thing here is that 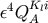 and
and 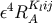 are at most
are at most 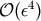 in
in
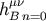 .
.
Finally, since the order of 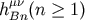 is higher than that of
is higher than that of 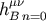 , we conclude that
, we conclude that
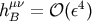 .
.
4.2.2 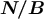 contribution
contribution
As far as the 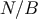 contribution is concerned, since the integrand
contribution is concerned, since the integrand 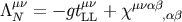 is at least
quadratic in the small deviation field
is at least
quadratic in the small deviation field 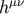 , we make the post-Newtonian expansion in the integrand.
Then, basically, with the help of (super-)potentials
, we make the post-Newtonian expansion in the integrand.
Then, basically, with the help of (super-)potentials 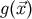 which satisfy
which satisfy 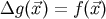 ,
, 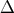 denoting the Laplacian, we have for each integral (see e.g. the
denoting the Laplacian, we have for each integral (see e.g. the  term in Equation (77))
term in Equation (77))
Equation (101) can be derived without using Dirac delta distributions (see Appendix B of [91 ]). For the
]). For the 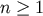 terms in
Equation (77), we use potentials many times to convert all the volume integrals into surface integrals and “
terms in
Equation (77), we use potentials many times to convert all the volume integrals into surface integrals and “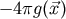 ”
terms.
”
terms.
In fact finding the super-potentials is one of the most formidable tasks especially when we proceed to
high post-Newtonian orders. Fortunately, up to 2.5 PN order, all the required super-potentials are
available. At 3 PN order, there appear many integrands for which we could not find the required
super-potentials. To obtain the 3 PN equations of motion, we devise an alternative method similar to
the method employed by Blanchet and Faye [28 ]. The details of the method will be explained
later.
]. The details of the method will be explained
later.
Now the lowest order integrands can be evaluated with the body zone contribution 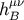 , and since
, and since
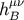 is
is 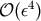 , we find
, we find
where we expanded 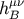 in an
in an  series,
Similarly, in the following we expand
series,
Similarly, in the following we expand 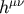 in an
in an  series. From these equations we find that
the deviation field in
series. From these equations we find that
the deviation field in 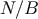 ,
, 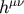 , is
, is 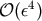 . (It should be noted that in the body zone
. (It should be noted that in the body zone
 is assumed to be of order unity and within our method we can not calculate
is assumed to be of order unity and within our method we can not calculate  there
explicitly. To obtain
there
explicitly. To obtain 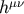 in the body zone, we have to know the internal structure of the
star.)
in the body zone, we have to know the internal structure of the
star.)
![]() , and from
elsewhere,
, and from
elsewhere, ![]() . Schematically we evaluate the following two types of integrals (we omit indices of the
field),
. Schematically we evaluate the following two types of integrals (we omit indices of the
field), ![]() in the body zone. For example, the
in the body zone. For example, the ![]() part in Equation (76
part in Equation (76![]() ),
), ![]() , gives
, gives
![]() ), we have
), we have
![]() ), we find that the body zone contributions,
), we find that the body zone contributions,
![]() , are of order
, are of order ![]() . Note that if we can not or do not assume the (nearly) stationarity of the
initial data for the stars, then, instead of Equation (88
. Note that if we can not or do not assume the (nearly) stationarity of the
initial data for the stars, then, instead of Equation (88![]() ) we have
) we have ![]() , we have to evaluate the surface integrals
, we have to evaluate the surface integrals ![]() . Generally, in
. Generally, in
![]() the moments
the moments ![]() and
and ![]() appear formally at the order
appear formally at the order ![]() and
and ![]() . Thus
. Thus ![]() and
and ![]() appear as
appear as ![]() is higher than that of
is higher than that of ![]() , we conclude that
, we conclude that
![]() .
.
![]() contribution is concerned, since the integrand
contribution is concerned, since the integrand ![]() is at least
quadratic in the small deviation field
is at least
quadratic in the small deviation field ![]() , we make the post-Newtonian expansion in the integrand.
Then, basically, with the help of (super-)potentials
, we make the post-Newtonian expansion in the integrand.
Then, basically, with the help of (super-)potentials ![]() which satisfy
which satisfy ![]() ,
, ![]() denoting the Laplacian, we have for each integral (see e.g. the
denoting the Laplacian, we have for each integral (see e.g. the ![]() term in Equation (77
term in Equation (77![]() ))
))
![]() ]. The details of the method will be explained
later.
]. The details of the method will be explained
later.
![]() , and since
, and since
![]() is
is ![]() , we find
, we find