Volume 4,
Issue 2, 2003
Article
37
|
INEQUALITIES RELATED TO REARRANGEMENTS OF POWERS AND SYMMETRIC POLYNOMIALS
CEZAR JOITA AND
PANTELIMON STANICA
DEPARTMENT OF MATHEMATICS,
LEHIGH UNIVERSITY,
BETHLEHEM, PA 18015, USA.
E-Mail: cej3@lehigh.edu
URL: http://www.lehigh.edu/~cej3/cej3.html
AUBURN UNIVERSITY MONTGOMERY,
DEPARTMENT OF MATHEMATICS,
MONTGOMERY,
AL 36124-4023, USA.
E-Mail: pstanica@mail.aum.edu
URL: http://sciences.aum.edu/~stanica
Received 29 April, 2003; Accepted 19 May, 2003.
Communicated by: C. Niculescu
|
ABSTRACT.
In [2] the second author proposed to find a description
(or examples) of real-valued 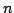 -variable functions satisfying the
following two inequalities: -variable functions satisfying the
following two inequalities:
if
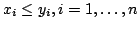 , then , then
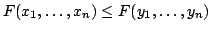 , , |
|
with strict inequality if there is an index 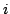 such that such that 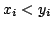 ; and for ; and for
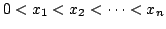 , then,
In this short note we extend in a direction a result of [2] and we
prove a theorem that provides a large class of examples satisfying
the two inequalities, with , then,
In this short note we extend in a direction a result of [2] and we
prove a theorem that provides a large class of examples satisfying
the two inequalities, with  replaced by any symmetric
polynomial with positive coefficients. Moreover, we find that the
inequalities are not specific to expressions of the form replaced by any symmetric
polynomial with positive coefficients. Moreover, we find that the
inequalities are not specific to expressions of the form 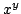 ,
rather they hold for any function ,
rather they hold for any function 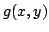 that satisfies some
conditions. A simple consequence of this result is a theorem of
Hardy, Littlewood and Polya [1]. that satisfies some
conditions. A simple consequence of this result is a theorem of
Hardy, Littlewood and Polya [1].
[1] G. HARDY, J.E. LITTLEWOOD and G. PÓLYA, Inequalities, Cambridge Univ. Press, 2001.
[2] P. STANICA, Inequalities on linear functions and circular
powers, J. Ineq. in Pure and Applied Math., 3(3) (2002),
Art. 43.
Key words:
Symmetric Polynomials, Permutations, Inequalities.
2000 Mathematics Subject
Classification:
05E05, 11C08, 26D05.
|
|
|
Download this article (PDF):
|
Suitable for a printer: 
Suitable for a monitor:
 |
To view these files we
recommend you save them to your file system and then view by using
the Adobe Acrobat Reader.
That is, click on the icon using the 2nd mouse button and
select "Save Target As..." (Microsoft Internet
Explorer) or "Save Link As..." (Netscape
Navigator).
See our PDF pages for more
information.
|
|
|
|
Other issues
-
Volume 1, Issue 1, 2000
-
Volume 1, Issue
2, 2000
-
Volume 2, Issue
1, 2001
-
Volume 2, Issue
2, 2001
-
Volume 2, Issue
3, 2001
-
Volume 3, Issue
1, 2002
-
Volume 3, Issue
2, 2002
-
Volume 3, Issue
3, 2002
-
Volume 3, Issue
4, 2002
-
Volume 3, Issue
5, 2002
-
Volume 4, Issue
1, 2003
-
Volume 4, Issue
2, 2003
-
Volume 4, Issue
3, 2003
-
Volume 4, Issue
4, 2003
-
Volume 4, Issue
5, 2003
|
|

