7.1 Strengths and weaknesses
The main advantage of spectral methods, especially with respect to finite difference ones, is the very
rapid convergence of the numerical approximation to the real function. This implies that very high accuracy
can usually be reached with only a moderate number of points. This obviously makes the codes both faster
and less demanding on memory. Various examples of convergence can be found in Section 2. However,
this rapid convergence is only achieved for 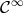 functions. Indeed, when the functions are
less continuous, spurious oscillations appear and the convergence only follows a power law. In
the case of discontinuous functions, this is known as the Gibbs phenomenon (see the extreme
case of Figure 11). Gibbs-like phenomena are very likely to prevent codes from converging
or to make time evolutions unstable. So spectral methods must rely heavily on the domain
decomposition of space and the domains must be chosen so that the various discontinuities lie at the
boundaries. Because of this, spectral methods are usually more difficult to implement than standard
finite differences (see, for instance, the intricate mappings of [7
functions. Indeed, when the functions are
less continuous, spurious oscillations appear and the convergence only follows a power law. In
the case of discontinuous functions, this is known as the Gibbs phenomenon (see the extreme
case of Figure 11). Gibbs-like phenomena are very likely to prevent codes from converging
or to make time evolutions unstable. So spectral methods must rely heavily on the domain
decomposition of space and the domains must be chosen so that the various discontinuities lie at the
boundaries. Because of this, spectral methods are usually more difficult to implement than standard
finite differences (see, for instance, the intricate mappings of [7 ]). The situation is even more
complicated when the surfaces of discontinuities are not known in advance or have complicated
shapes.
]). The situation is even more
complicated when the surfaces of discontinuities are not known in advance or have complicated
shapes.
Spectral methods are also very efficient at dealing with problems that are related to coordinate
singularities. Indeed, if the basis functions fulfill the regularity requirements, then all the functions will
automatically satisfy them. In particular, it makes the use of spherical coordinates much easier than with
other methods, as explained in Section 3.2.
Another nice feature is the fact that a function can be represented either by its coefficients or its values
at the collocation points. Depending on the operation one has to perform, it is easier to work with the one
representation or the other. When working in the coefficient space, one takes full advantage of the
nonlocality of the spectral representation. A lot of operations that would be difficult otherwise can then be
easily performed, like computing the ratio of two quantities vanishing at the same point (see, for
instance, [81]).