1.1 About spectral methods
When doing simulations and solving PDEs, one faces the problem of representing and deriving functions
on a computer, which deals only with (finite) integers. Let us take a simple example of a function
![f : [− 1,1] → ℝ](article0x.gif) . The most straightforward way to approximate its derivative is through finite-difference
methods: first one must setup a grid
. The most straightforward way to approximate its derivative is through finite-difference
methods: first one must setup a grid
![{xi}i=0...N ⊂ [− 1,1 ]](article1x.gif) of
of
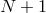 points in the interval, and represent
points in the interval, and represent  by its
by its 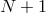 values on these grid points
values on these grid points
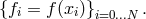 Then, the (approximate) representation of the derivative
Then, the (approximate) representation of the derivative 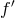 shall be, for instance,
If we suppose an equidistant grid, so that
shall be, for instance,
If we suppose an equidistant grid, so that 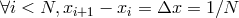 , the error in the
approximation (1) will decay as
, the error in the
approximation (1) will decay as 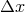 (first-order scheme). One can imagine higher-order schemes, with
more points involved for the computation of each derivative and, for a scheme of order
(first-order scheme). One can imagine higher-order schemes, with
more points involved for the computation of each derivative and, for a scheme of order 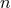 , the accuracy
can vary as
, the accuracy
can vary as 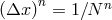 .
.
Spectral methods represent an alternate way: the function 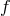 is no longer represented through its values
on a finite number of grid points, but using its coefficients (coordinates)
is no longer represented through its values
on a finite number of grid points, but using its coefficients (coordinates) 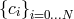 in a finite basis of
known functions
in a finite basis of
known functions 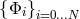
A relatively simple case is, for instance, when 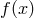 is a periodic function of period two, and the
is a periodic function of period two, and the
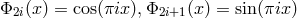 are trigonometric functions. Equation (2) is then nothing but the
truncated Fourier decomposition of
are trigonometric functions. Equation (2) is then nothing but the
truncated Fourier decomposition of  . In general, derivatives can be computed from the
. In general, derivatives can be computed from the  ’s, with the
knowledge of the expression for each derivative
’s, with the
knowledge of the expression for each derivative 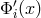 as a function of
as a function of 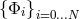 . The
decomposition (2) is approximate in the sense that
. The
decomposition (2) is approximate in the sense that 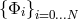 represent a complete basis of some
finite-dimensional functional space, whereas
represent a complete basis of some
finite-dimensional functional space, whereas 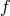 usually belongs to some other infinite-dimensional space.
Moreover, the coefficients
usually belongs to some other infinite-dimensional space.
Moreover, the coefficients 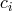 are computed with finite accuracy. Among the major advantages of using
spectral methods is the rapid decay of the error (faster than any power of
are computed with finite accuracy. Among the major advantages of using
spectral methods is the rapid decay of the error (faster than any power of 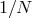 , and in practice often
exponential
, and in practice often
exponential 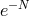 ), for well-behaved functions (see Section 2.4.4); one, therefore, has an infinite-order
scheme.
), for well-behaved functions (see Section 2.4.4); one, therefore, has an infinite-order
scheme.
In a more formal and mathematical way, it is useful to work within the methods of weighted residuals
(MWR, see also Section 2.5). Let us consider the PDE
where 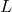 is a linear operator,
is a linear operator, 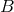 the operator defining the boundary conditions and
the operator defining the boundary conditions and  is a source term.
A function
is a source term.
A function 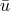 is said to be a numerical solution of this PDE if it satisfies the boundary conditions (4) and
makes “small” the residual
If the solution is searched for in a finite-dimensional subspace of some given Hilbert space (any relevant
is said to be a numerical solution of this PDE if it satisfies the boundary conditions (4) and
makes “small” the residual
If the solution is searched for in a finite-dimensional subspace of some given Hilbert space (any relevant
 space) in terms of the expansion (2), then the functions
space) in terms of the expansion (2), then the functions 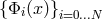 are called trial functions
and, in addition, the choice of a set of test functions
are called trial functions
and, in addition, the choice of a set of test functions 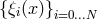 defines the notion of smallness for the
residual by means of the Hilbert space scalar product
Within this framework, various numerical methods can be classified according to the choice of the trial
functions:
defines the notion of smallness for the
residual by means of the Hilbert space scalar product
Within this framework, various numerical methods can be classified according to the choice of the trial
functions:
- Finite differences: the trial functions are overlapping local polynomials of fixed order (lower
than
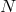 ).
).
- Finite elements: the trial functions are local smooth functions, which are nonzero, only on
subdomains of
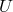 .
.
- Spectral methods: the trial functions are global smooth functions on
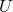 .
.
Various choices of the test functions define different types of spectral methods, as detailed in
Section 2.5. Usual choices for the trial functions are (truncated) Fourier series, spherical harmonics or
orthogonal families of polynomials.
![]() is no longer represented through its values
on a finite number of grid points, but using its coefficients (coordinates)
is no longer represented through its values
on a finite number of grid points, but using its coefficients (coordinates) ![]() in a finite basis of
known functions
in a finite basis of
known functions ![]()