B.4 Spin geodesic precession
The spin precession can be evaluated using the following equation:
Evaluating the surface integrals in 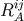 and
and 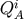 (appearing through the momentum-velocity relation),
we have up to
(appearing through the momentum-velocity relation),
we have up to  Note that there is no monopole-monopole coupling.
Note that there is no monopole-monopole coupling.
In our formalism, the above form is sufficient since we use 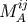 , not the spin vector
, not the spin vector 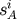 . To transform
the above equation into the usual form, we take a “crude” method; we shall treat one star, say, the star 1 as
if it felt only the gravitational field of the companion star. Motivated by the formalism on extended bodies
by Dixon [69], we introduce the intrinsic spin four-vector
. To transform
the above equation into the usual form, we take a “crude” method; we shall treat one star, say, the star 1 as
if it felt only the gravitational field of the companion star. Motivated by the formalism on extended bodies
by Dixon [69], we introduce the intrinsic spin four-vector  and the intrinsic spin tensor
and the intrinsic spin tensor 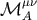 as
as
where 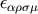 is the totally anti-symmetric symbol with
is the totally anti-symmetric symbol with 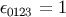 .
. 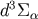 is the proper volume element
satisfying
is the proper volume element
satisfying ![d3Σ [αuA β] = 0](article1096x.gif) .
. 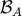 is a three-sphere surrounding star
is a three-sphere surrounding star 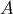 whose normal is
whose normal is 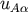 and whose
radius is
and whose
radius is 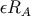 .
. 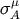 is the spacelike four-vector satisfying
is the spacelike four-vector satisfying  . The four-momentum is
normalized as
. The four-momentum is
normalized as  . The above definitions imply the spin supplementary condition
where
. The above definitions imply the spin supplementary condition
where 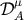 is the intrinsic dipole moment. Now we construct a coordinate transformation from the near
zone
is the intrinsic dipole moment. Now we construct a coordinate transformation from the near
zone 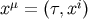 to the Fermi normal coordinates
to the Fermi normal coordinates 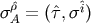 (see e.g. Section 40.7 in [122
(see e.g. Section 40.7 in [122 ]),
Then we express the intrinsic spin tensor in the Fermi normal coordinates in terms of the moments in the
near zone. Using
]),
Then we express the intrinsic spin tensor in the Fermi normal coordinates in terms of the moments in the
near zone. Using 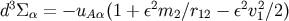 , we have
Now defining the intrinsic center of mass by setting
, we have
Now defining the intrinsic center of mass by setting 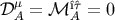 , we obtain
Notice that this relation provides the spin-orbit coupling force in the previous form (see Appendix B.1; thus
we get
, we obtain
Notice that this relation provides the spin-orbit coupling force in the previous form (see Appendix B.1; thus
we get 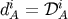 in the present treatment). Using Equation (228), we finally obtain the spin
geodesic equation in the usual form (we omit the quadrupole and
in the present treatment). Using Equation (228), we finally obtain the spin
geodesic equation in the usual form (we omit the quadrupole and 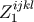 term for simplicity),
where
term for simplicity),
where 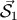 is the spatial part of the intrinsic spin four-vector
is the spatial part of the intrinsic spin four-vector 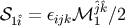 . Equation (239) is the
geodesic precession equation, or called the de Sitter-Fokker precession (see e.g. Section 40.7 in [122]
and [36, 145]).
. Equation (239) is the
geodesic precession equation, or called the de Sitter-Fokker precession (see e.g. Section 40.7 in [122]
and [36, 145]).
![]() , not the spin vector
, not the spin vector ![]() . To transform
the above equation into the usual form, we take a “crude” method; we shall treat one star, say, the star 1 as
if it felt only the gravitational field of the companion star. Motivated by the formalism on extended bodies
by Dixon [69], we introduce the intrinsic spin four-vector
. To transform
the above equation into the usual form, we take a “crude” method; we shall treat one star, say, the star 1 as
if it felt only the gravitational field of the companion star. Motivated by the formalism on extended bodies
by Dixon [69], we introduce the intrinsic spin four-vector ![]() and the intrinsic spin tensor
and the intrinsic spin tensor ![]() as
as