B.1 Spin-orbit coupling force
It is well known that the definition of a dipole moment of the star, which we equate to zero to determine
the center of mass of the star, affects the appearance of the spin-orbit coupling force (see e.g. [108
]). If one
chooses 
as in [94], the corresponding spin-orbit coupling force takes the usual form [46, 108, 152]
where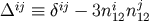 
and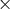 
in this section denotes the outer product for the usual Euclidean
spatial three-vectors. The spin vector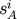 
is defined by
where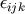 
is the totally antisymmetric symbol.
![k F i |i = − ε4V- [(2m M il+ m M il)Δlk + 2 (m M lk + m M lk)Δli] 1SO dA=0 r312 1 2 2 1 1 2 2 1 4m1 [ i ] = ε r3- 6(⃗s2 × ⃗n12) ⋅ ⃗Vn 12 + 4⃗s2 × ⃗V − 6⃗s2 × ⃗n12 (⃗n12 ⋅ ⃗V ) 12 [ ] +ε4m2- 6(⃗s1 × ⃗n12) ⋅ ⃗V ni12 + 3⃗s1 × ⃗V − 3⃗s1 × ⃗n12(⃗n12 ⋅ ⃗V ) , (221 ) r312](article1071x.gif)
