5.1 Cosmological light-cone effect on the two-point correlation functions
Observing a distant patch of the Universe is equivalent to observing the past. Due to the finite light
velocity, a line-of-sight direction of a redshift survey is along the time, as well as spatial, coordinate axis.
Therefore the entire sample does not consist of objects on a constant-time hypersurface, but rather on a
light-cone, i.e., a null hypersurface defined by observers at 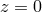 . This implies that many properties of the
objects change across the depth of the survey volume, including the mean density, the amplitude of spatial
clustering of dark matter, the bias of luminous objects with respect to mass, and the intrinsic evolution of
the absolute magnitude and spectral energy distribution. These aspects should be properly taken
into account in order to extract cosmological information from observed samples of redshift
surveys.
. This implies that many properties of the
objects change across the depth of the survey volume, including the mean density, the amplitude of spatial
clustering of dark matter, the bias of luminous objects with respect to mass, and the intrinsic evolution of
the absolute magnitude and spectral energy distribution. These aspects should be properly taken
into account in order to extract cosmological information from observed samples of redshift
surveys.
In order to predict quantitatively the two-point statistics of objects on the light-cone, one must take
account of
- nonlinear gravitational evolution,
- linear redshift-space distortion,
- nonlinear redshift-space distortion,
- weighted averaging over the light-cone,
- cosmological redshift-space distortion due to the geometry of the Universe, and
- object-dependent clustering bias.
The Effect 5 comes from our ignorance of the correct cosmological parameters, and Effect 6 is rather sensitive
to the objects which one has in mind. Thus the latter two effects will be discussed in the next
Section 5.2.
Nonlinear gravitational evolution of mass density fluctuations is now well understood, at least for
two-point statistics. In practice, we adopt an accurate fitting formula [67 ] for the nonlinear power spectrum
] for the nonlinear power spectrum
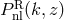 in terms of its linear counterpart. If one assumes a scale-independent deterministic linear bias,
furthermore, the power spectrum distorted by the peculiar velocity field is known to be well approximated
by the following expression:
in terms of its linear counterpart. If one assumes a scale-independent deterministic linear bias,
furthermore, the power spectrum distorted by the peculiar velocity field is known to be well approximated
by the following expression:
where 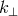 and
and 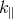 are the comoving wavenumber perpendicular and parallel to the line-of-sight of an
observer, and
are the comoving wavenumber perpendicular and parallel to the line-of-sight of an
observer, and 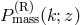 is the mass power spectrum in real space. The second factor on the r.h.s. comes
from the linear redshift-space distortion [38], and the last factor is a phenomenological correction for the
non-linear velocity effect [67
is the mass power spectrum in real space. The second factor on the r.h.s. comes
from the linear redshift-space distortion [38], and the last factor is a phenomenological correction for the
non-linear velocity effect [67 ]. In the above, we introduce
]. In the above, we introduce
We assume that the pair-wise velocity distribution in real space is approximated by
with 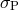 being the 1-dimensional pair-wise peculiar velocity dispersion. Then the finger-of-God effect is
modeled by the damping function
being the 1-dimensional pair-wise peculiar velocity dispersion. Then the finger-of-God effect is
modeled by the damping function ![[ ] Dvel k∥σP (z)](article587x.gif) :
where
:
where 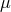 is the direction cosine in
is the direction cosine in 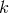 -space, and the dimensionless wavenumber
-space, and the dimensionless wavenumber  is related to the
peculiar velocity dispersion
is related to the
peculiar velocity dispersion 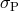 in the physical velocity units:
in the physical velocity units:
Since we are mainly interested in the scales around 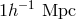 , we adopt the following fitting formula
throughout the analysis below which better approximates the small-scale dispersions in physical units:
, we adopt the following fitting formula
throughout the analysis below which better approximates the small-scale dispersions in physical units:
Integrating Equation (131) over 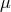 , one obtains the direction-averaged power spectrum in redshift
space:
, one obtains the direction-averaged power spectrum in redshift
space:
where
Adopting those approximations, the direction-averaged correlation functions on the light-cone are finally
computed as
where 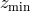 and
and 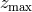 denote the redshift range of the survey, and
denote the redshift range of the survey, and
Throughout the present analysis, we assume a standard Robertson–Walker metric of the form
where 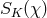 is determined by the sign of the curvature
is determined by the sign of the curvature 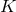 as
where the present scale factor
as
where the present scale factor 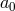 is normalized as unity, and the spatial curvature
is normalized as unity, and the spatial curvature 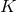 is given as
(see Equation (13)). The radial comoving distance
is given as
(see Equation (13)). The radial comoving distance 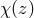 is computed by
is computed by
The comoving angular diameter distance 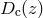 at redshift
at redshift  is equivalent to
is equivalent to 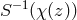 , and, in
the case of
, and, in
the case of 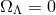 , is explicitly given by Mattig’s formula:
, is explicitly given by Mattig’s formula:
Then 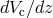 , the comoving volume element per unit solid angle, is explicitly given as
, the comoving volume element per unit solid angle, is explicitly given as
![]() ] for the nonlinear power spectrum
] for the nonlinear power spectrum
![]() in terms of its linear counterpart. If one assumes a scale-independent deterministic linear bias,
furthermore, the power spectrum distorted by the peculiar velocity field is known to be well approximated
by the following expression:
in terms of its linear counterpart. If one assumes a scale-independent deterministic linear bias,
furthermore, the power spectrum distorted by the peculiar velocity field is known to be well approximated
by the following expression: ![]() , we adopt the following fitting formula
throughout the analysis below which better approximates the small-scale dispersions in physical units:
, we adopt the following fitting formula
throughout the analysis below which better approximates the small-scale dispersions in physical units:
![]() ) over
) over ![]() , one obtains the direction-averaged power spectrum in redshift
space:
, one obtains the direction-averaged power spectrum in redshift
space: ![]() at redshift
at redshift ![]() is equivalent to
is equivalent to ![]() , and, in
the case of
, and, in
the case of ![]() , is explicitly given by Mattig’s formula:
, is explicitly given by Mattig’s formula: