Volume 4,
Issue 3 (GI8), 2003
Article
60
|
ON ZEROS OF RECIPROCAL POLYNOMIALS OF ODD DEGREE
PIROSKA LAKATOS AND
LÁSZLÓ LOSONCZI
INSTITUTE OF MATHEMATICS,
DEBRECEN UNIVERSITY,
4010 DEBRECEN, PF.12, HUNGARY.
E-Mail: lapi@math.klte.hu
E-Mail: losi@math.klte.hu
Received 12 December, 2002; Accepted 30 July, 2003.
Communicated by: A. Sofo
|
ABSTRACT.
The first author [1] proved that all zeros of the reciprocal
polynomial
of degree 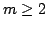 with real coefficients with real coefficients
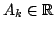 (i.e.
(i.e. 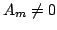 and and
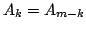 for all for all
![$ k=0,\dots,\left[\frac{m}{2}\right]$](../abstract/143_02_ab/img6.gif) ) are on the unit circle,
provided that
Moreover, the zeros of ) are on the unit circle,
provided that
Moreover, the zeros of 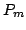 are near to the are near to the 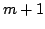 st roots of
unity (except the root st roots of
unity (except the root 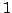 ). A. Schinzel [3] generalized the first
part of Lakatos' result for self-inversive polynomials i.e.
polynomials
for which ). A. Schinzel [3] generalized the first
part of Lakatos' result for self-inversive polynomials i.e.
polynomials
for which
 and and
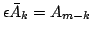 for all for all
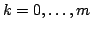 with a fixed with a fixed
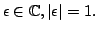 He proved that all zeros of He proved that all zeros of 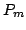 are
on the unit circle, provided that
If the inequality is strict the zeros are
single. The aim of this paper is to show that for real reciprocal
polynomials of odd degree Lakatos' result remains valid even if
We conjecture that Schinzel's result can also be extended
similarly: all zeros of are
on the unit circle, provided that
If the inequality is strict the zeros are
single. The aim of this paper is to show that for real reciprocal
polynomials of odd degree Lakatos' result remains valid even if
We conjecture that Schinzel's result can also be extended
similarly: all zeros of 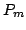 are on the unit circle if are on the unit circle if 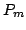 is
self-inversive and is
self-inversive and
[1] P. LAKATOS, On zeros of reciprocal polynomials, Publ.
Math. (Debrecen) 61 (2002), 645-661.
[3] A. SCHINZEL, Self-inversive polynomials with all zeros on the
unit circle, Ramanujan Journal, to appear.
Key words:
Reciprocal, Semi-reciprocal polynomials, Chebyshev transform,
Zeros on the unit circle.
2000 Mathematics Subject
Classification:
Primary 30C15, Secondary 12D10, 42C05.
|
|
|
Download this article (PDF):
|
Suitable for a printer: 
Suitable for a monitor:
 |
To view these files we
recommend you save them to your file system and then view by using
the Adobe Acrobat Reader.
That is, click on the icon using the 2nd mouse button and
select "Save Target As..." (Microsoft Internet
Explorer) or "Save Link As..." (Netscape
Navigator).
See our PDF pages for more
information.
|
|
|
|
Other issues
-
Volume 1, Issue 1, 2000
-
Volume 1, Issue
2, 2000
-
Volume 2, Issue
1, 2001
-
Volume 2, Issue
2, 2001
-
Volume 2, Issue
3, 2001
-
Volume 3, Issue
1, 2002
-
Volume 3, Issue
2, 2002
-
Volume 3, Issue
3, 2002
-
Volume 3, Issue
4, 2002
-
Volume 3, Issue
5, 2002
-
Volume 4, Issue
1, 2003
-
Volume 4, Issue
2, 2003
-
Volume 4, Issue
3, 2003
-
Volume 4, Issue
4, 2003
-
Volume 4, Issue
5, 2003
|
|

