|
ABSTRACT. An extension of the Bojanic-Stanojevic type inequality [1] is
made by considering the 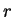 -th derivate of the Dirichlet's kernel -th derivate of the Dirichlet's kernel
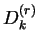 instead of instead of 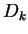 .
Namely, the following inequality is proved: .
Namely, the following inequality is proved:
where
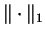 is the is the 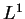 -norm, { -norm, {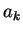 } is a sequence of real numbers, } is a sequence of real numbers,
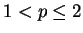 , ,
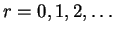 and and 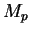 is
an absolute constant dependent only on is
an absolute constant dependent only on 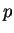 . As an application of this
inequality, it is shown that the class . As an application of this
inequality, it is shown that the class 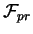 is a subclass of is a subclass of
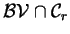 , where , where 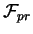 is the extension of
the Fomin's class, is the extension of
the Fomin's class,  is the extension of the
Garrett-Stanojevic class [8] and is the extension of the
Garrett-Stanojevic class [8] and
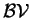 is the class of all
null sequences of bounded variation. is the class of all
null sequences of bounded variation.
[1] R. BOJANIC and C.V.
STANOJEVIC, A class of L1-convergence, Trans. Amer. Math.
Soc., 269 (1982), 677-683.
[8] Z. TOMOVSKI, An extension of the Garrett- Stanojevic class, Approx.
Theory Appl., 16(1) (2000) 46–51. [ONLINE] A corrected version is
available in the RGMIA Research Report Collection, 3(4), Article
3, 2000. URL: http://rgmia.vu.edu.au/v3n4.html
Key words:
Bojanic-Stanojevic inequality, Sidon-Fomin's
inequality, Bernstein's
inequality,
L1-convergence,
cosine series.
2000 Mathematics Subject
Classification: 26D15,
42A20.
|
|

