
| Appendixes for 'Applications of a New Property of Conics to Architecture: An Alternative Design Project for Rio de Janeiro Metropolitan Cathedral' |
|---|
APPENDIX I.
DEFINITION OF THE CONIC ELLIPSE
The
ellipse as a conic section can be considered as generated by
the cutting of a cone by a plane that cuts all its generating
lines, and it is therefore defined as the loci of points of the
plane whose sum of distances between two points is constant.
 |
|
|
Taking into account the ellipse illustrated in the Figure I.1, the following points are defined:
- The fixed points F, F', are called focus of the ellipse;
- The distance
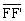 =
2c is called focal length;
=
2c is called focal length;
- The distances
 and
and
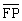 are
called radius vectors;
are
called radius vectors;
- The sum
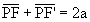 ,
is a constant value, as it can be demonstrated according to the
definition for the ellipse itself;
,
is a constant value, as it can be demonstrated according to the
definition for the ellipse itself;
- The difference
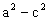 will
be called b2 and will be positive, since a2
> c2;
will
be called b2 and will be positive, since a2
> c2;
- The line segment distance
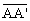 =
2a will be called major axis of the ellipse;
=
2a will be called major axis of the ellipse;
- The line segment distance
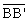 =2b,
will be called minor axis of the ellipse.
=2b,
will be called minor axis of the ellipse.
Taking the line segment ![]() as
the horizontal axis and the perpendicular to the point in the
middle of the line segment
as
the horizontal axis and the perpendicular to the point in the
middle of the line segment ![]() as
the vertical axis (figure I.1), and from the definition of the
ellipse given above, it comes to:
as
the vertical axis (figure I.1), and from the definition of the
ellipse given above, it comes to:
|
|
By operating upon that equation and, taking into account the relation a2-c2=b2, the following expression is obtained for the canonical equation of the ellipse:
|
|
(I.1) |
APPENDIX II.
SURFACES AND CURVES ON A SURFACE [Granero
Rodriguez 1985]
In
the affine three-space, the term curves applies to the entire
collection of points C Ì Â3 of coordinates
(x(t), y(t), z(t)), such that x(t), y(t), z(t) are continuous
functions at a certain interval I.
Hence, the equations:
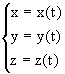 |
(II.1) |
are called the parametric equations of the curve C (tridimensional line).
Considering the existing isomorphism between the free vectors
of space and the points of E3, it is often more suitable
to define curve C by a free vector ![]() of
components (x(t), y(t), z(t)).
of
components (x(t), y(t), z(t)).
In this case it is clear (Figure II.1) that by changing the parameter t, the vector end will draw the curve C.
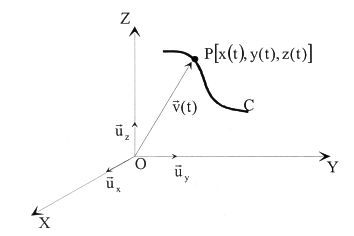 |
|
|
The equation ![]() is called vectorial equation of C.
is called vectorial equation of C.
When the curve is located in a plane is called a plane curve. Otherwise it is called a nonplane curve.
In the affine three-space the term surface applies to the entire collection of points S Ì Â3 of coordinates [x (l, m), y(l,m), z(l,m)], such that x(l,m), y(l,m), z(l,m) are continuous functions in a certain domain D Í Â2 .
The equations
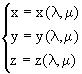 |
(II.2) |
are called parametric equations of the surface S.
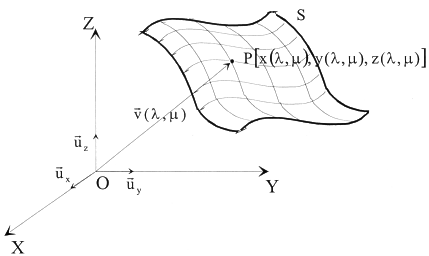
In the same way, based on the isomorphism between free vectors
and points, we would be able to define the surface S by a free
vector or position vector ![]() of
components (x(l,m), y(l,m),
z(l,m)). In these conditions (Figure
II.2), by varying the parameters l
and m, the position vector end will
travel through the surface S.
of
components (x(l,m), y(l,m),
z(l,m)). In these conditions (Figure
II.2), by varying the parameters l
and m, the position vector end will
travel through the surface S.
 |
|
|
The equation ![]() will be called the vectorial equation of such a surface.
will be called the vectorial equation of such a surface.
Often it is feasible to remove the two parameters l and m among the three equations (II.2), giving rise to an equation of the form F(x,y,z) = 0, or z = f(x,y), which is called the Cartesian equation of the surface. Reciprocally, if the surface is defined by z = f(x,y), making x = l, y = m yieds the following parametric equations
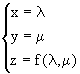 |
(II.3) |
Likewise, let us notice that whatever relationship is established
between both parameters, as for instance l
= f(m), the position vector ![]() will
depend solely on one of those parameters, and consequently, a
curve upon the surface will be drawn. Again from what has preceded,
the result will be that when one of the two parameters is fixed,
or when these are in the relationship l
= f(m), or
will
depend solely on one of those parameters, and consequently, a
curve upon the surface will be drawn. Again from what has preceded,
the result will be that when one of the two parameters is fixed,
or when these are in the relationship l
= f(m), or ![]() ,
which is the same, we will have a curve on the surface.
,
which is the same, we will have a curve on the surface.
Example:
Given the surface S defined in parametrics as:
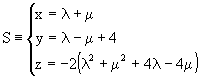 |
by isolating l and m in terms of x and y between the two first equations, which are linear, by substituting the third we will have z = f(x,y). However in this case we can very easily obtain z = f(x,y) by just noticing that:
|
|
where ![]() .
.
Therefore, ![]() or
or
![]() represents
the Cartesian equation of the surface.
represents
the Cartesian equation of the surface.
It is very simple to display the preceding surface, since all its intersections through planes z = k parallel to the horizontal are circumferences the radii of which become uniformly shorter until becoming null at point (0,0,16).
Likewise, let us notice that
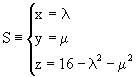
are less dificult parametric equations of this surface than the preceding ones.
APPENDIX III.
RULED SURFACES [Granero Rodriguez
1985]
It
is well known from analytic geometry that every straight line
in space can be expressed in the form:
|
|
(III.1) |
where m ,n,a,b Î Â.
It is clear that when the coefficients m,n,a,b are fixed,
the system (III.1) will represent a unique straight line in space,
or in other words, that to every quadruple set of (m,n,a,b) Î Â4 will correspond
a unique straight line in such a space.
If we make this four coefficients be in terms of a parameter
z Î Â, then for every
value of z we will have a well-defined
straight line such that by varying this parameter the result
will be a loci of straight lines, that is, in a surface made
up of straight lines.
A ruled surface is that which is generated by a straight line (generating line) which moves according to a given mathematical law.
Let (III.1) be a variable straight line whose coefficients m,n,a,b depend on a parameter z.
In these conditions we will have that the equations:
|
|
(III.2) |
which represent the parametric equations of a surface (two equations with a sole parameter whose isolation will give raise to the Cartesian form).
 |
|
|
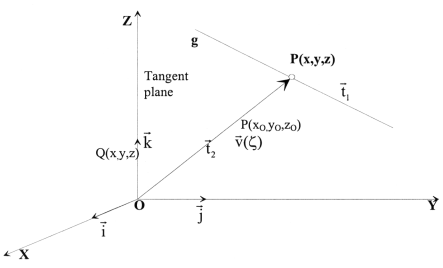
Since the vectorial equation of the surface is defined by means of the position vector of a given point P(x,y,z) (Figure III.1), we have:
|
|
where
|
|
will be its vectorial equation. Hence we will be able to say:
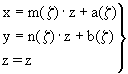 |
(III.3) |
are also parametric equations for that surface.
Let us note that last equation of the preceding system can be verified by every point of space and in consequence z = z will be all Â3.
It is clear that the parametric equations (III.2) and (III.3) represent the same surface, since the system (III.3) can be considered as intersection of the surface defined as the system (III,2) with z=z, that is, with Â3.
Furthermore, taking into account that APPENDIX II demonstrated the parametrical expression of the surfaces through three equations with two parameters l and m, in this paper we have choosen to achieve it with system (III,3), and for convenience t and z have been selected as parameters.
REFERENCES
Granero-Rodríguez, Francisco. 1985. Álgebra
y geometría analítica. Madrid and Mexico City:McGraw-Hill.
|
J.V. Martín Zorraquino, Francisco Granero Rodríguez and José Luis Cano Martín, "Appendixes for 'Applications of a New Property of Conics to Architecture: An Alternative Design Project for Rio de Janeiro Metropolitan Cathedral'"], Nexus Network Journal, vol. 3, no. 2 (Spring 2001), http://www.nexusjournal.com/MarGraCan-App.html |
