As I was preparing for my trip to Egypt last year, I took some time the night before to do a drawing of the Great Pyramid of Khufu at Giza. As I developed my sketch into a rough two point perspective, I realized that there are actually three triangles in the half base of the elevation, but we see only one. The other two are overlapped by the first.

Most of us are aware of the elevation of the pyramid, but what are we actually seeing when we look at this profile? In the following drawings, I will demonstrate the relationships of the three triangles, and show a triangle that I've never seen in any of my readings on the subject. For the purposes of clarity in the column, I will call this third triangle, "MR Triangle1". This arrangement of ratios, even though I found them, has physically existed at least back to the builders' drawings for Khufu's Pyramid. Potentially, the relationship has existed for a very long time, as long as the universe has. Geometric relationships were present in the cosmos before human life, as we know it on the Earth, began and developed. As such, in this construction, there is a natural "marriage of incommensurables". They are: f, Öf, Ö2, and 1/f.

PROCEDURE
1. Figure 1.1 shows the construction of the golden section rectangle using the half diagonal of the square, Ö 5 ÷ 2. Therefore, T2G : GO :: f : 1. GT2 is then rotated to the opposite side of the golden section rectangle to become Öf at T2a. O becomes the half base of the pyramid. The right, scalene triangle that results from this rotation has sides: a.) 1 (the half base); b.) Öf (the cathetus, the vertical, or the altitude), and f (the hypotenuse). This triangle is sometimes referred to as the "Triangle of Price" (TP), after Professor Price, and is the only right, scalene triangle whose sides are in a geometric progression, based on Öf, 1.2720196…

2. Figure 1.1a shows the plan of the pyramid projected into a two point perspective. This view provides us with the three triangles. They are:
I. Triangle TP, GT2O (Öf) ;
II. Triangle MR1, ZT2O (this is the triangle that I stumbled upon.); and,
III. Triangle MR2, ZT2N (f, as half of a golden section rectangle, cut along its diagonal).

3. Figure 1.2 shows the separation of the three right, scalene triangles from the pyramid and their three different ratios. Basically, however, the marriage is between the two systems: the f family and Ö2.

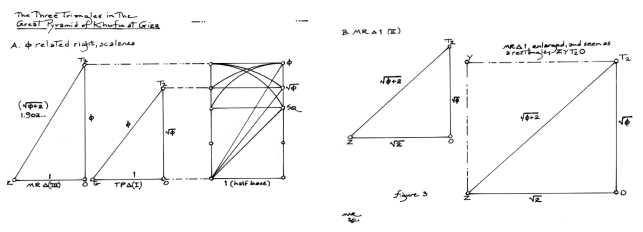4. Figure 1.3 shows each of the three triangles, their ratios, and their measures.

The important things to note are that physically, when we observe the sloped elevation of the pyramid - the triangular plane that conceals the other two triangles behind it - we are seeing the three components of the golden section rectangle, i.e., short side,1, long side,f, and, the diagonal, 1.902…, or, Öf + 2. This diagonal is the actual sloping edge of the pyramid. The Triangle of Price is concealed by both the f half-rectangle in front, and the diagonally positioned MR1 triangle. This is the third, sandwiched triangle whose base runs along the diagonal of the square in the half base. When working out the ratios, this third rectangle shares the diagonal of the f rectangle, the 1.902…, which is the sloping edge of the pyramid. Instead of using the sides of the square in the half base, as the f and Öf ratios do, it uses the diagonal of a square, or,Ö2. Two of the three major divisions of the square are exhibited in this marriage: 1) the half-diagonal for the golden section; 2) the whole diagonal for the Ö2; and 3) whole numbers/fractional parts. What we have here is an example of a natural, geometric relationship where nothing has been built, forced, bent, or removed. Perhaps this is why the marriage has lasted for at over 2500 years, a bit longer than even the successful ones today!