2.3 Explicit calculation in harmonic coordinates
Here we shall use the above formalism to make an explicit calculation in harmonic coordinates. The
reduced Einstein equations in the harmonic condition are written as
where
where 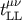 is the Landau–Lifshitz pseudotensor [115
is the Landau–Lifshitz pseudotensor [115 ]. In this section we shall choose an isentropic perfect
fluid for
]. In this section we shall choose an isentropic perfect
fluid for  which is enough for most applications,
where
which is enough for most applications,
where 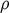 is the rest mass density,
is the rest mass density, 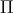 the internal energy,
the internal energy, 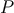 the pressure, and
the pressure, and 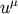 the four-velocity of
the fluid with normalization
The conservation of energy and momentum is expressed as
the four-velocity of
the fluid with normalization
The conservation of energy and momentum is expressed as
Defining the gravitational field variable as
where 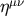 is the Minkowski metric, the reduced Einstein equations (14) and the gauge condition (15)
take the following form:
Thus the characteristics are determined by the operator
is the Minkowski metric, the reduced Einstein equations (14) and the gauge condition (15)
take the following form:
Thus the characteristics are determined by the operator 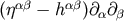 , and thus the light cone deviates
from that in the flat spacetime. We may use this form of the reduced Einstein equations in the calculation
of the waveform far away from the source because the deviation plays a fundamental role there [12].
However, in the study of the gravitational field near the source it is not necessary to consider the deviation
of the light cone from the flat one and thus it is convenient to use the following form of the reduced Einstein
equations [5]:
where
Equations (23) and (24) together imply the conservation law
We shall take as our variables the set
, and thus the light cone deviates
from that in the flat spacetime. We may use this form of the reduced Einstein equations in the calculation
of the waveform far away from the source because the deviation plays a fundamental role there [12].
However, in the study of the gravitational field near the source it is not necessary to consider the deviation
of the light cone from the flat one and thus it is convenient to use the following form of the reduced Einstein
equations [5]:
where
Equations (23) and (24) together imply the conservation law
We shall take as our variables the set 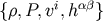 , with the definition
The time component of four-velocity
, with the definition
The time component of four-velocity 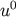 is determined from Equation (19). To make a well-defined system
of equations we must add the conservation law for the number density
is determined from Equation (19). To make a well-defined system
of equations we must add the conservation law for the number density 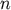 , which is some function of the
density
, which is some function of the
density 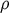 and pressure
and pressure 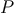 :
Equations (27) and (29) imply that the flow is adiabatic. The role of the equation of state is played by the
arbitrary function
:
Equations (27) and (29) imply that the flow is adiabatic. The role of the equation of state is played by the
arbitrary function  .
.
Initial data for the above set of equations are 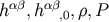 , and
, and 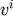 , but not all these data are
independent because of the existence of the constraint equations. Equations (23) and (24) imply the four
constraint equations among the initial data for the field,
, but not all these data are
independent because of the existence of the constraint equations. Equations (23) and (24) imply the four
constraint equations among the initial data for the field,
where 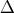 is the Laplacian in the flat space. We shall choose
is the Laplacian in the flat space. We shall choose 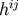 and
and 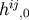 as free data and solve
Equation (30) for
as free data and solve
Equation (30) for  and Equation (23) for
and Equation (23) for 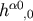 . Of course these constraints cannot be
solved explicitly, since
. Of course these constraints cannot be
solved explicitly, since 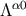 contains
contains 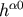 , but they can be solved iteratively as explained below. As
discussed above, we shall assume that the free data
, but they can be solved iteratively as explained below. As
discussed above, we shall assume that the free data  and
and 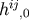 for the field vanish. One can show that
such initial data satisfy the O’Murchadha and York criterion for the absence of radiation far away from the
source [124].
for the field vanish. One can show that
such initial data satisfy the O’Murchadha and York criterion for the absence of radiation far away from the
source [124].
In the actual calculation, it is convenient to use an expression with explicit dependence of  .
The harmonic condition allows us to have such an expression in terms of the retarded integral,
.
The harmonic condition allows us to have such an expression in terms of the retarded integral,
where 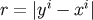 and
and  is the past flat light cone of the event
is the past flat light cone of the event  in the spacetime given
by
in the spacetime given
by  , truncated where it intersects with the initial hypersurface
, truncated where it intersects with the initial hypersurface 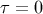 .
. 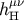 is the unique solution of
the homogeneous wave equation in the flat spacetime,
is the unique solution of
the homogeneous wave equation in the flat spacetime,
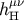 evolves from a given initial data on the
evolves from a given initial data on the 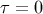 initial hypersurface which are subject to the
constraint equations (30). The explicit form of
initial hypersurface which are subject to the
constraint equations (30). The explicit form of  is available via the Poisson formula (see e.g. [144
is available via the Poisson formula (see e.g. [144 ]),
]),
We shall henceforth ignore the homogeneous solutions because they play no important role. Because of
the  dependence of the integral region, the domain of integral is finite as long as
dependence of the integral region, the domain of integral is finite as long as 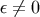 and their
diameter increases like
and their
diameter increases like 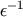 as
as 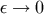 .
.
Given the formal expression (31) in terms of initial data (9), we can take the Lie derivative and
evaluate these derivatives at  . The Lie derivative is nothing but a partial derivative with respect to
. The Lie derivative is nothing but a partial derivative with respect to
 in the coordinate system for the fiber bundle given by
in the coordinate system for the fiber bundle given by 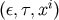 . Accordingly one should convert all the
time indices to
. Accordingly one should convert all the
time indices to  indices. For example,
indices. For example, 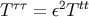 which is of order
which is of order 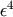 , since
, since 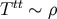 is of order
is of order
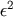 . Similarly the other components of stress-energy tensor
. Similarly the other components of stress-energy tensor  and
and 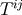 are of order
are of order 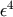 as
well. Thus we expect that the first nonvanishing derivative in Equation (31) will be the forth derivative. In
fact we find
as
well. Thus we expect that the first nonvanishing derivative in Equation (31) will be the forth derivative. In
fact we find
where we have adopted the notation
and
In the above calculation we have taken the point of view that 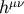 is a tensor field, defined by giving
its components in the assumed harmonic coordinates as the difference between the tensor density
is a tensor field, defined by giving
its components in the assumed harmonic coordinates as the difference between the tensor density 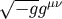 and
and 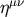 .
.
The conservation law (27) also has its first nonvanishing derivatives at this order, which are
Equations (34), (40), and (41) constitute Newtonian theory of gravity. Thus the lowest nonvanishing
derivative with respect to  is indeed Newtonian theory, and the 1 PN and 2 PN equations emerge from
the sixth and eighth derivatives, respectively, in the conservation law (27). At the next derivative, the
quadrupole radiation reaction term emerges.
is indeed Newtonian theory, and the 1 PN and 2 PN equations emerge from
the sixth and eighth derivatives, respectively, in the conservation law (27). At the next derivative, the
quadrupole radiation reaction term emerges.
![]() , and
, and ![]() , but not all these data are
independent because of the existence of the constraint equations. Equations (23
, but not all these data are
independent because of the existence of the constraint equations. Equations (23![]() ) and (24
) and (24![]() ) imply the four
constraint equations among the initial data for the field,
) imply the four
constraint equations among the initial data for the field, ![]() .
The harmonic condition allows us to have such an expression in terms of the retarded integral,
.
The harmonic condition allows us to have such an expression in terms of the retarded integral,
![]() dependence of the integral region, the domain of integral is finite as long as
dependence of the integral region, the domain of integral is finite as long as ![]() and their
diameter increases like
and their
diameter increases like ![]() as
as ![]() .
.
![]() ) in terms of initial data (9
) in terms of initial data (9![]() ), we can take the Lie derivative and
evaluate these derivatives at
), we can take the Lie derivative and
evaluate these derivatives at ![]() . The Lie derivative is nothing but a partial derivative with respect to
. The Lie derivative is nothing but a partial derivative with respect to
![]() in the coordinate system for the fiber bundle given by
in the coordinate system for the fiber bundle given by ![]() . Accordingly one should convert all the
time indices to
. Accordingly one should convert all the
time indices to ![]() indices. For example,
indices. For example, ![]() which is of order
which is of order ![]() , since
, since ![]() is of order
is of order
![]() . Similarly the other components of stress-energy tensor
. Similarly the other components of stress-energy tensor ![]() and
and ![]() are of order
are of order ![]() as
well. Thus we expect that the first nonvanishing derivative in Equation (31
as
well. Thus we expect that the first nonvanishing derivative in Equation (31![]() ) will be the forth derivative. In
fact we find
) will be the forth derivative. In
fact we find ![]() is a tensor field, defined by giving
its components in the assumed harmonic coordinates as the difference between the tensor density
is a tensor field, defined by giving
its components in the assumed harmonic coordinates as the difference between the tensor density ![]() and
and ![]() .
.
![]() ) also has its first nonvanishing derivatives at this order, which are
) also has its first nonvanishing derivatives at this order, which are