C.2 Equations of motion
Let us start explaining again our situation and discuss the strong field point particle limit [81]. A small
spherical compact object with mass 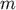 moves at an arbitrary speed around a massive body with mass
moves at an arbitrary speed around a massive body with mass
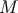 . We would like to find the equations of motion for the object including radiation reaction. We assume
that the object is stationary except for higher order tidal effects, so that we can safely neglect the emission
of gravitational waves from the object itself, but of course we cannot neglect the gravitational waves emitted
by the orbital motion of the object. We denote the world line of the center of mass of the object
as
. We would like to find the equations of motion for the object including radiation reaction. We assume
that the object is stationary except for higher order tidal effects, so that we can safely neglect the emission
of gravitational waves from the object itself, but of course we cannot neglect the gravitational waves emitted
by the orbital motion of the object. We denote the world line of the center of mass of the object
as 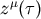 and define the body zone of the object as follows. We imagine a spherical region
around
and define the body zone of the object as follows. We imagine a spherical region
around 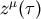 and a radius that scales as
and a radius that scales as  . At the same time we scale the linear dimension
of the object as
. At the same time we scale the linear dimension
of the object as 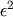 so that the boundary of the body zone is located at the far zone of the
object. Namely we are able to have a multipole expansion of the field generated by the object
at the surface of the body zone. We also implicitly assume that the mass of the object scales
as
so that the boundary of the body zone is located at the far zone of the
object. Namely we are able to have a multipole expansion of the field generated by the object
at the surface of the body zone. We also implicitly assume that the mass of the object scales
as  so that the compactness of the object remains constant in the point particle limit as
so that the compactness of the object remains constant in the point particle limit as
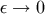 . This is why we call this limit the strong field point particle limit. Then we calculate the
metric perturbation induced by the small object in this limit. The smallness parameter
. This is why we call this limit the strong field point particle limit. Then we calculate the
metric perturbation induced by the small object in this limit. The smallness parameter  has a
dimension of length which characterizes the smallness of the object. One may regard it as the ratio
between the physical scale of the object and the characteristic scale of the background curvature.
We assume that the background metric
has a
dimension of length which characterizes the smallness of the object. One may regard it as the ratio
between the physical scale of the object and the characteristic scale of the background curvature.
We assume that the background metric 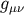 satisfies the Einstein equations in vacuum. So
the Ricci tensor of the background vanishes. Since we have assumed that the mass scale of
the small object is much smaller than the scale of the gravitational field of the background
geometry, we approximate the metric perturbation by the linear perturbation of the small particle
satisfies the Einstein equations in vacuum. So
the Ricci tensor of the background vanishes. Since we have assumed that the mass scale of
the small object is much smaller than the scale of the gravitational field of the background
geometry, we approximate the metric perturbation by the linear perturbation of the small particle
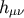 .
.
We will work in the harmonic gauge,
where the semicolon means that the covariant derivative with respect to the background metric and the
trace-reversed variable is defined as usual,
Then the linearized Einstein equations take the following form:
This can be solved formally as follows,
where we have used the retarded tensor Green’s function defined by
For the general tensor Green’s function and the definition of 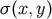 ,
, 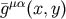 ,
, 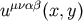 ,
,
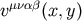 , and
, and 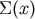 , please refer to Mino et al. [121] and DeWitt and Brehme [68].
, please refer to Mino et al. [121] and DeWitt and Brehme [68].
Now we take the point particle limit. In this limit the above metric perturbation contains terms of
different  dependence which makes the calculation of the equations of motion simple. For example, terms
with negative powers of
dependence which makes the calculation of the equations of motion simple. For example, terms
with negative powers of  appear from the Dirac delta distribution part of the Green’s function:
appear from the Dirac delta distribution part of the Green’s function:
As explained below we only need the field on the boundary of the body zone which is the far zone of the
body itself, and thus we may make use of the multipole expansion for the field. For this purpose we choose
our coordinate system as follows,
where 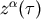 is the world line of the center of the object. The center is assumed to be always
inside the body in the point particle limit, and thus there is no ambiguity for the choice of the
center. In this coordinate system the volume element satisfies
is the world line of the center of the object. The center is assumed to be always
inside the body in the point particle limit, and thus there is no ambiguity for the choice of the
center. In this coordinate system the volume element satisfies 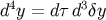 . Thus we have
where
. Thus we have
where 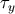 is the retarded time of each point
is the retarded time of each point 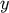 . Then the multipole expansion is obtained by expanding
the above expression at the retarded time of the center of the object
. Then the multipole expansion is obtained by expanding
the above expression at the retarded time of the center of the object 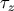 defined by
defined by 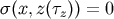 . This
can be easily done by noticing the condition
. This
can be easily done by noticing the condition 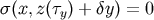 . Then the difference between
. Then the difference between 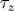 and
and
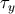 is given by
Using this
is given by
Using this 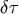 we can expand
we can expand 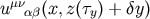 around
around 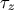 . In principle we can calculate arbitrarily
high multipole moments in this way. Here we only calculate the leading term. Then we only need
. In principle we can calculate arbitrarily
high multipole moments in this way. Here we only calculate the leading term. Then we only need
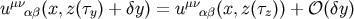 , and
, and 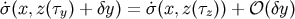 . By defining
the mass as follows,
we finally obtain the following expression for
. By defining
the mass as follows,
we finally obtain the following expression for 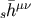 :
:
Now we derive the equations of motion using this expression. First we define the  dependent
four-momentum of the object as the volume integral of the effective stress-energy tensor
dependent
four-momentum of the object as the volume integral of the effective stress-energy tensor 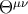 over the
body zone
over the
body zone 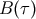 ,
,
Since the effective stress-energy tensor satisfies the conservation law 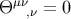 , the change of the
four-momentum defined above may be expressed as the surface integral over the boundary of the body zone
, the change of the
four-momentum defined above may be expressed as the surface integral over the boundary of the body zone
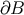 ,
where
,
where 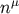 is the unit normal to the surface and
is the unit normal to the surface and 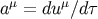 is the four-acceleration. The equations of
motion are obtained by taking the point particle limit of
is the four-acceleration. The equations of
motion are obtained by taking the point particle limit of 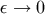 . Thus we need to calculate
. Thus we need to calculate 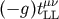 on
the body zone boundary (field points) on which the multipole expansion of the self-field and the Taylor
expansion of the nonsingular part of the field are available, and to pick up only terms of order
on
the body zone boundary (field points) on which the multipole expansion of the self-field and the Taylor
expansion of the nonsingular part of the field are available, and to pick up only terms of order 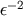 in the
expression. All the other terms but one term, which is proportional to
in the
expression. All the other terms but one term, which is proportional to 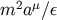 and can be
renormalized to the mass of the small object, vanish in the limit or the angular integration.
Remembering that the LL tensor is bilinear in the Christoffel symbols and the Christoffel symbols
are the derivatives of the metric tensor, one may realize that the only remaining terms come
from the combination of the 0th order of the smooth part of the metric and
and can be
renormalized to the mass of the small object, vanish in the limit or the angular integration.
Remembering that the LL tensor is bilinear in the Christoffel symbols and the Christoffel symbols
are the derivatives of the metric tensor, one may realize that the only remaining terms come
from the combination of the 0th order of the smooth part of the metric and 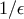 part of the
self-field which is given by Equation (252). The remaining part of the self-field is the so-called tail
part that is regular at the object which is the only relevant point in our calculation. The field
point
part of the
self-field which is given by Equation (252). The remaining part of the self-field is the so-called tail
part that is regular at the object which is the only relevant point in our calculation. The field
point 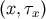 is now on the body zone boundary, which is defined by
is now on the body zone boundary, which is defined by 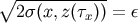 and
and
Using this expression we have the following result in the point particle limit,
where the Christoffel symbols here are calculated in terms of the smooth part of the metric 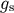 . Then the
ADM mass is related to the four-momentum as follows, which is supported by the higher order
post-Newtonian approximation [91
. Then the
ADM mass is related to the four-momentum as follows, which is supported by the higher order
post-Newtonian approximation [91 , 95, 91]:
Finally we have
which is the geodesic equation on the geometry determined by the smooth part of the metric around the
compact object.
, 95, 91]:
Finally we have
which is the geodesic equation on the geometry determined by the smooth part of the metric around the
compact object.
In fact, the spin effect on the equations of motion can be derived in a similar way and the standard
result [152] can be obtained.
We have proved that a small compact object moves on the geodesic determined by only the smooth part
of the geometry around the object. Thus the equations of motion are automatically obtained by
determining the geometry around the object which is of course an implicit functional of the world
line of the object. The smooth part contains the gravitational waves emitted by the orbital
motion so that this equation includes the damping force due to radiation reaction. Our method
avoids using a singular source in the first place by making use of the strong field point particle
limit. All the quantities should be evaluated at the surface of the body zone boundary and
thus we only need the dependence of the distance from the center of the object, namely the
 dependence of the field. In this way we are able to avoid using any divergent quantities
in any part of our calculation. This strongly suggests that our method may be used to get
unique equations of fast motion with radiation reaction. This will be investigated in future
publications.
dependence of the field. In this way we are able to avoid using any divergent quantities
in any part of our calculation. This strongly suggests that our method may be used to get
unique equations of fast motion with radiation reaction. This will be investigated in future
publications.
In this section, we have assumed spherical symmetry of the compact object except for the tidal effect. It
is straightforward to generalize the case to multipole moments in our formalism. This will also be studied in
future publications.
![]() dependence which makes the calculation of the equations of motion simple. For example, terms
with negative powers of
dependence which makes the calculation of the equations of motion simple. For example, terms
with negative powers of ![]() appear from the Dirac delta distribution part of the Green’s function:
appear from the Dirac delta distribution part of the Green’s function:
![]() dependent
four-momentum of the object as the volume integral of the effective stress-energy tensor
dependent
four-momentum of the object as the volume integral of the effective stress-energy tensor ![]() over the
body zone
over the
body zone ![]() ,
, ![]() dependence of the field. In this way we are able to avoid using any divergent quantities
in any part of our calculation. This strongly suggests that our method may be used to get
unique equations of fast motion with radiation reaction. This will be investigated in future
publications.
dependence of the field. In this way we are able to avoid using any divergent quantities
in any part of our calculation. This strongly suggests that our method may be used to get
unique equations of fast motion with radiation reaction. This will be investigated in future
publications.