4.5 Halo occupation function approach for galaxy biasing
Since the clustering of dark matter halos is well understood now, one can describe the galaxy biasing if
the halo model is combined with the relation between the halos and luminous objects. This is another
approach to galaxy biasing, halo occupation function (HOF), which has become very popular recently.
Indeed the basic idea behind HOF has a long history, but the model predictions have been significantly
improved with the recent accurate models for the mass function, the biasing and the density profile of dark
matter halos. We refer the readers to an extensive review on the HOF by Cooray and Sheth [13]. Here we
briefly outline this approach.
We adopt a simple parametric form for the average number of a given galaxy population as a function of
the hosting halo mass:
The above statistical and empirical relation is the essential ingredient in the current modeling characterized
by the minimum mass 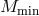 of halos which host the population of galaxies, a normalization parameter
which can be interpreted as the critical mass
of halos which host the population of galaxies, a normalization parameter
which can be interpreted as the critical mass 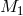 above which halos typically host more than one
galaxy (note that
above which halos typically host more than one
galaxy (note that 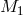 may exceed
may exceed 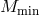 since the above relation represents the statistical
expected value of number of galaxies), and the power-law index
since the above relation represents the statistical
expected value of number of galaxies), and the power-law index 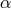 of the mass dependence of the
efficiency of galaxy formation. We will put constraints on the three parameters from the observed
number density and clustering amplitude for each galaxy population. In short, the number
density of galaxies is most sensitive to
of the mass dependence of the
efficiency of galaxy formation. We will put constraints on the three parameters from the observed
number density and clustering amplitude for each galaxy population. In short, the number
density of galaxies is most sensitive to 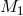 which changes the average number of galaxies per
halo. The clustering amplitude on large scales is determined by the hosting halos and thus very
sensitive to the mass of those halos,
which changes the average number of galaxies per
halo. The clustering amplitude on large scales is determined by the hosting halos and thus very
sensitive to the mass of those halos, 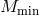 . The clustering on smaller scales, on the other
hand, depends on those three parameters in a fairly complicated fashion; roughly speaking,
. The clustering on smaller scales, on the other
hand, depends on those three parameters in a fairly complicated fashion; roughly speaking,
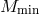 changes the amplitude, while
changes the amplitude, while 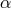 , and to a lesser extent
, and to a lesser extent 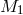 as well, change the
slope.
as well, change the
slope.
With the above relation, the number density of the corresponding galaxy population at redshift  is
given by
is
given by
where 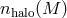 denotes the halo mass function.
denotes the halo mass function.
The galaxy two-point correlation function on small scales is dominated by contributions of galaxy pairs
located in the same halo. For instance, Bullock et al. [8] adopted the mean number of galaxy pairs
 within a halo of mass
within a halo of mass 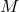 of the form:
of the form:
In the framework of the halo model, the galaxy power spectrum consists of two contributions, one from
galaxy pairs located in the same halo (1-halo term) and the other from galaxy pairs located in two different
halos (2-halo term):
The 1-halo term is written as
Seljak [77 ] chose
] chose 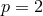 for
for  and
and 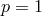 for
for 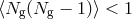 . The 2-halo term on
the assumption of the linear halo bias model [59
. The 2-halo term on
the assumption of the linear halo bias model [59 ] reduces to
where
] reduces to
where 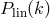 is the linear dark matter power spectrum,
is the linear dark matter power spectrum, 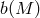 is the halo bias factor, and
is the halo bias factor, and
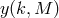 is the Fourier transform of the halo dark matter profile normalized by its mass,
is the Fourier transform of the halo dark matter profile normalized by its mass,
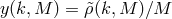 [77].
[77].
The halo occupation formalism, although simple, provides a useful framework in deriving constraints on
galaxy formation models from large data sets of the upcoming galaxy redshift surveys. For example, Zehavi
et al. [105] used the halo occupation formalism to model departures from a power law in the SDSS galaxy
correlation function. They demonstrated that this is due to the transition from a large-scale regime
dominated by galaxy pairs in different halos to a small-scale regime dominated by those in
the same halo. Magliocchetti and Porciani [47] applied the halo occupation formalism to the
2dFGRS clustering results per spectral type of Madgwick et al. [45 ]. This provides constraints on
the distribution of late-type and early-type galaxies within the dark matter halos of different
mass.
]. This provides constraints on
the distribution of late-type and early-type galaxies within the dark matter halos of different
mass.
![]() is
given by
is
given by ![]() within a halo of mass
within a halo of mass ![]() of the form:
of the form: ![]() ]. This provides constraints on
the distribution of late-type and early-type galaxies within the dark matter halos of different
mass.
]. This provides constraints on
the distribution of late-type and early-type galaxies within the dark matter halos of different
mass.