USA-Chile Workshop on Nonlinear Analysis,
Electron. J. Diff. Eqns., Conf. 06, 2001, pp. 243-255.
On a fourth order superlinear elliptic problem
M. Ramos & P. Rodrigues
Abstract:
We prove the existence of a nonzero solution for the fourth order
elliptic equation
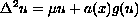
with boundary conditions
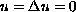 .
Here,
.
Here,
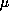 is a real parameter,
is a real parameter,
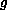 is superlinear
both at zero and infinity and
is superlinear
both at zero and infinity and
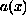 changes sign in
changes sign in
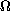 .
The proof uses a variational argument based on the argument
by Bahri-Lions [3].
.
The proof uses a variational argument based on the argument
by Bahri-Lions [3].
Published January 1, 2001.
Math Subject Classifications: 35J25, 35J20, 58E05.
Key Words: Superlinear elliptic problems, Morse index, biharmonic operator.
Show me the DVI(48K),
PDF(152K),
TEX and other files for this article.
Miguel Ramos
CMAF, Universidade de Lisboa
Av. Prof. Gama Pinto, 2
1649-003 Lisboa, Portugal
e-mail: mramos@lmc.fc.ul.pt
Paula Rodrigues
FCT, Universidade Nova de Lisboa
Quinta da Torre
2825 Monte da Caparica, Portugal
e-mail: paula.p.rodrigues@netc.pt
Return to the EJDE web page
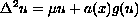
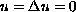 .
Here,
.
Here,
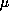 is a real parameter,
is a real parameter,
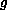 is superlinear
both at zero and infinity and
is superlinear
both at zero and infinity and
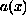 changes sign in
changes sign in
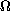 .
The proof uses a variational argument based on the argument
by Bahri-Lions [3].
.
The proof uses a variational argument based on the argument
by Bahri-Lions [3].