Кирьяцкий Э. Г.
Оценки вещественных коэффициентов Тейлора в одном классе функцийРассматривается класс
аналитических в единичном круге функций F(z) = zn + a2,nzn+1 + a3,nzn+2 + … , для которых n-я разделенная разность [F(z); z0, … , zn] отлична от нуля при любых z0, … , zn
E и am,n
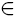
. Установлена справедливость неравенства |ak,n+2| ≤ (kγk,n − 1)/(γk,n + k − 2), γk,n = max |ak,n|. Если n — нечетное число, то γk,n = (n + k − 1)/(n + 1).
Kir’yatskii E. G.
Estimates for the real taylor coefficients in one function classConsidering the class
of analytic functions F(z) = zn + a2,nzn+1 + a3,nzn+2 + … in the unit disk with am,n
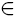
and the nonvanishing nth divided difference [F(z); z0, … , zn] for all z0, … , zn
E we establish that |ak,n+2| ≤ (kγk,n − 1)/(γk,n + k − 2), where γk,n = max |ak,n|. If n is an odd number then γk,n = (n + k − 1)/(n + 1).
Полный текст статьи / Full texts:
- PDF file (425 KB)
- PostScript file (770 KB)
![]()
Адрес редакции:
пр. Коптюга, 4,
Новосибирск 630090.
Телефон: (383-2) 333-493
E-mail: smz@math.nsc.ru