Романов В. Г.
О гладкости фундаментального решения для гиперболического уравнения второго порядкаДля линейного гиперболического дифференциального уравнения второго порядка с переменными коэффициентами, зависящими от пространственной переменной x
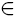
n, рассматривается задача о построении фундаментального решения. В предположении, что коэффициенты уравнения обладают достаточно высокой, но конечной гладкостью, выписывается структура фундаментального решения, устанавливается гладкость коэффициентов разложения сингулярной части решения и характеризуется гладкость его регулярной части.
Romanov V. G.
On smoothness of a fundamental solution to a second order hyperbolic equationWe consider the problem of constructing a fundamental solution to a second order hyperbolic linear equation with variable coefficients depending on the space variable x
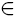
n. Under the assumption of high but finite smoothness of the coefficients, we write out the structure of a fundamental solution, establish smoothness of the coefficients of the expansion of its singular part, and characterize smoothness of the regular part.
Полный текст статьи / Full texts:
- PDF file (410 KB)
- PostScript file (740 KB)
![]()
Адрес редакции:
пр. Коптюга, 4,
Новосибирск 630090.
Телефон: (383-2) 333-493
E-mail: smz@math.nsc.ru