Ли Я., Цяо Ш., Ван Я. 
Замечание о теореме Скибы

Подгруппу H группы G называют слабо s-перестановочной в G, если существует субнормальная подгруппа T в G такая, что G = HT и H ∩ T ≤ H_sG, где H_sG  — максимальная s-перестановочная подгруппа в G, содержащаяся в H. Замечательный результат А. Н. Скибы улучшает
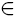
Теорема. Пусть  — насыщенная формация, содержащая класс всех сверхразрешимых групп , и G — группа с E в качестве нормальной подгруппы в G такая, что G/E . Предположим, что каждая нециклическая силовская p-подгруппа P в F*(E) имеет подгруппу D такую, что 1 < |D| < |P| и все подгруппы H в P порядка |H| = |D| слабо s-перестановочны в G для любого p π (F*(E)). Кроме того, предположим, что все циклические подгруппы в P порядка 4 слабо s-перестановочны в G, если P — неабелева 2-группа и |D| = 2. Тогда G .

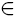
Li Y., Qiao Sh., Wang Y.
A note on a result of Skiba

A subgroup H of a group G is called weakly s-permutable in G if there is a subnormal subgroup T of G such that G = HT and H ∩ T ≤ H_sG, where H_sG is the maximal s-permutable subgroup of G contained in H. We improve a nice result of Skiba to get the following
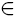
Theorem. Let be a saturated formation containing the class of all supersoluble groups and let G be a group with E a normal subgroup of G such that G/E . Suppose that each noncyclic Sylow p-subgroup P of F*(E) has a subgroup D such that 1 < |D| < |P| and all subgroups H of P with order |H| = |D| are weakly s-permutable in G for all p π (F*(E)); moreover, we suppose that every cyclic subgroup of P of order 4 is weakly s-permutable in G if P is a nonabelian 2-group and |D| = 2. Then G .

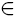
Полный текст статьи / Full texts:

• PDF file (410 KB)
• PostScript file (765 KB)