6.1 Meaning of 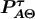
In this section we explain the meaning of 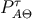 . First of all, we expand in an
. First of all, we expand in an  series the
four-velocity of star
series the
four-velocity of star 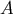 normalized as
normalized as 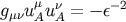 , where
, where 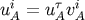 . The result is
The field should be evaluated somehow at
. The result is
The field should be evaluated somehow at 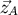 . This is a formal series since the metric derived via the
point particle description diverges at
. This is a formal series since the metric derived via the
point particle description diverges at  .
.
Now let us regularize this equation with the Hadamard partie finie regularization (see [88, 143] and for
example, [26 , 30] in the literature of the post-Newtonian approximation). Consider a function
, 30] in the literature of the post-Newtonian approximation). Consider a function 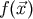 which
can be expanded around
which
can be expanded around 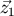 in the form
in the form
Then the Hadamard partie finie at 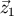 of the function
of the function 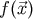 is defined by
is defined by
For example, by this procedure 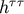 becomes (see Equation (130))
becomes (see Equation (130))
for star  . In the above equation,
. In the above equation, ![H [f]A](article711x.gif) means that we regularize the quantity
means that we regularize the quantity  at star
at star 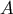 by the
Hadamard partie finie. Evaluating Equation (152) and
by the
Hadamard partie finie. Evaluating Equation (152) and ![√ --- H [ − g]A](article714x.gif) by this procedure, then comparing the
result to Equation (148) combined with Equations (149, 150, 151), we find at least up to 3 PN order:
It is important that even after regularizing all the divergent terms, there remains a nonlinear effect.
Equation (156) is natural. And note that we have never assumed this relation in advance. This relation has
been derived by solving the evolution equation for
by this procedure, then comparing the
result to Equation (148) combined with Equations (149, 150, 151), we find at least up to 3 PN order:
It is important that even after regularizing all the divergent terms, there remains a nonlinear effect.
Equation (156) is natural. And note that we have never assumed this relation in advance. This relation has
been derived by solving the evolution equation for  functionally. In this regard, it is worth
mentioning that the naturality of Equation (156) supports the use of the Hadamard partie finie
regularization (or any regularization procedures if we can reproduce Equation (156) with them)
to derive the 3 PN mass-energy relation to deal with divergences when one uses Dirac delta
distributions.
functionally. In this regard, it is worth
mentioning that the naturality of Equation (156) supports the use of the Hadamard partie finie
regularization (or any regularization procedures if we can reproduce Equation (156) with them)
to derive the 3 PN mass-energy relation to deal with divergences when one uses Dirac delta
distributions.
Finally, we note that up to 3 PN order
is satisfied if we use the Hadamard partie finie regularization explained above.
![]() , 30] in the literature of the post-Newtonian approximation). Consider a function
, 30] in the literature of the post-Newtonian approximation). Consider a function ![]() which
can be expanded around
which
can be expanded around ![]() in the form
in the form ![]() becomes (see Equation (130
becomes (see Equation (130![]() ))
))