Constants of the form

$\begin{displaymath}C = \sum_{k=0}^\infty \frac{p(k)}{q(k)b^k} \end{displaymath}$

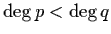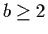where p and q are integer polynomials, $\deg p <\deg q$ , and p(k)/q(k) is non-singular for non-negative k and $b\geq 2$ , have special properties. The n^th digit (base b) of C may be calculated in (essentially) linear time without computing its preceding digits, and constants of this form are conjectured to be either rational or normal to base b.

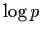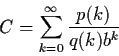
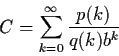
This paper constructs such formulae for constants of the form $\log p$ for many primes p. This holds for all Gaussian-Mersenne primes and for a larger class of ``generalized Guassian-Mersenne primes''. Finally, connections to Aurifeuillian factorizations are made.