Analogues of Up-down Permutations for Colored Permutations

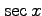
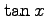
André proved that $\sec x$ is the generating function of all up-down permutations of even length and $\tan x$ is the generating function of all up-down permutation of odd length. There are three equivalent ways to define up-down permutations in the symmetric group

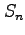
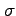
. That is, a permutation $\sigma$ in the symmetric group

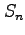
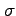
is an up-down permutation if either (i) the rise set of $\sigma$ consists of all the odd numbers less than

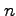
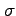
, (ii) the descent set of $\sigma$ consists of all even number less than

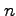
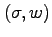
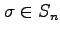
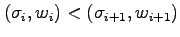
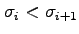
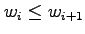
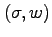
, or (iii) both (i) and (ii). We consider analogues of André's results for colored permutations of the form $(\sigma ,w)$ where $\sigma \in S_n$ and $w \in \{0,\ldots, k-1\}^n$ under the product order. That is, we define $(\sigma _i,w_i) < (\sigma _{i+1},w_{i+1})$ if and only if $\sigma _i < \sigma _{i+1}$ and $w_i \leq w_{i+1}$ . 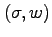We then say a colored permutation $(\sigma ,w)$ is (I) an up-not up permutation if the rise set of $(\sigma ,w)$ consists of all the odd numbers less than

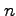
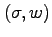
, (II) a not down-down permutation if the descent set of $(\sigma ,w)$ consists of all the even numbers less than

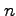
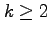
, (III) an up-down permutation if both (I) and (II) hold. For $k \geq 2$ , conditions (I), (II), and (III) are pairwise distinct. We find

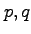
-analogues of the generating functions for up-not up, not down-down, and up-down colored permutations.

Analogues of Up-down Permutations for Colored Permutations

Andrew Niedermaier and Jeffrey Remmel Department of Mathematics University of California, San Diego La Jolla, CA 92093-0112 USA

Andrew Niedermaier and Jeffrey Remmel
Department of Mathematics
University of California, San Diego
La Jolla, CA 92093-0112
USA