How the Shift Parameter Affects the Behavior of a Family of Meta-Fibonacci Sequences

We explore the effect of different values of the shift parameter

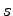
on the behavior of the family of meta-Fibonacci sequences defined by the

-term recursion

$\begin{displaymath}T_{s,k}(n) := \displaystyle\sum_{i=0}^{k-1} T_{s,k}(n - i - s - T_{s,k}(n - i - 1)), \quad n > s + k, \quad k \geq 2\end{displaymath}$

with the

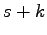
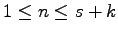
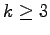
initial conditions $T_{s,k}(n) = 1$ for $1 \leq n \leq s + k$ . We show that for any odd $k \geq 3$ and non-negative integer

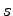
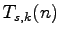
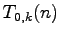
the values in the sequence $T_{s,k}(n)$ and $T_{0,k}(n)$ are essentially the same. The only differences in these sequences are that each power of

occurs precisely

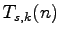
times in $T_{s,k}(n)$ and

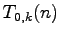
times in $T_{0,k}(n)$ . For even

the frequency of

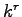
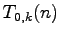
in $T_{0,k}(n)$ depends upon

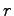
. We conjecture that for

even the effect of the shift parameter

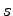
is analogous to that for

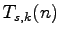
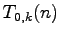
odd, in the sense that the only differences in the sequences $T_{s,k}(n)$ and $T_{0,k}(n)$ occur in the frequencies of the powers of

; specifically, each power of

appears to occur precisely

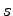
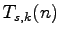
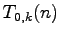
more times in $T_{s,k}(n)$ than it does in $T_{0,k}(n)$ .

Received June 2 2008; revised version received August 15 2008. Published in Journal of Integer Sequences, August 17 2008.

How the Shift Parameter Affects the Behavior of a Family of Meta-Fibonacci Sequences

Mu Cai and Stephen M. Tanny Department of Mathematics University of Toronto Toronto, Ontario M5S 2E4 Canada

Mu Cai and Stephen M. Tanny
Department of Mathematics
University of Toronto
Toronto, Ontario M5S 2E4
Canada