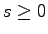
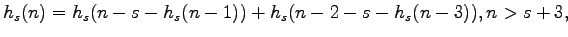
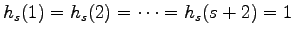
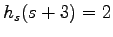
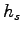
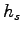
For any integer , we derive a combinatorial interpretation for the family of sequences generated by the recursion (parameterized by ) with the initial conditions and . We show how these sequences count the number of leaves of a certain infinite tree structure. Using this interpretation we prove that sequences are ``slowly growing'', that is, sequences are monotone nondecreasing, with successive terms increasing by 0 or 1, so each sequence hits every positive integer. 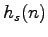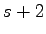Further, for fixed the sequence hits every positive integer twice except for powers of 2, all of which are hit times. Our combinatorial interpretation provides a simple approach for deriving the ordinary generating functions for these sequences.