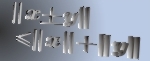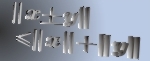| |
|
|
| |
Volume 4, Issue 3, Article 60 |
|
|
|
|
|
| |
On Zeros of Reciprocal Polynomials of Odd Degree
|
| |
|
Authors: |
Piroska Lakatos, Laszlo Losonczi, |
|
| |
|
Keywords:
|
Reciprocal, Semi-reciprocal polynomials, Chebyshev transform, Zeros on the unit circle. |
|
| |
|
Date Received:
|
12/12/02 |
|
| |
|
Date Published:
|
30/07/03 |
|
| |
|
Subject Codes: |
30C15, 12D10, 42C05.
|
|
| |
|
Editors: |
Anthony Sofo, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The first author [1] proved that all zeros of the reciprocal polynomial of degree  with real coefficients with real coefficients  (i.e. (i.e.  and and  for all for all  ) are on the unit circle, provided that Moreover, the zeros of ) are on the unit circle, provided that Moreover, the zeros of  are near to the are near to the
 st roots of unity (except the root st roots of unity (except the root  ). A. Schinzel [3] generalized the first part of Lakatos' result for self-inversive polynomials i.e. polynomials
for which ). A. Schinzel [3] generalized the first part of Lakatos' result for self-inversive polynomials i.e. polynomials
for which  and and  for all for all  with a fixed with a fixed  He proved that all zeros of He proved that all zeros of  are on the unit circle, provided that
If the inequality is strict the zeros are single. The aim of this paper is to show that for real reciprocal polynomials of odd degree Lakatos' result remains valid even if
We conjecture that Schinzel's result can also be extended similarly: all zeros of are on the unit circle, provided that
If the inequality is strict the zeros are single. The aim of this paper is to show that for real reciprocal polynomials of odd degree Lakatos' result remains valid even if
We conjecture that Schinzel's result can also be extended similarly: all zeros of
 are on the unit circle if are on the unit circle if
 is self-inversive and is self-inversive and
[1] P. LAKATOS, On zeros of reciprocal polynomials, Publ. Math. (Debrecen) 61 (2002), 645-661.
[3] A. SCHINZEL, Self-inversive polynomials with all zeros on the unit circle, Ramanujan Journal, to appear.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|