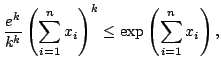JIPAM

Refinements of Inequalities Between the Sum of Squares and the Exponential of Sum of a Nonnegative Sequence  
 
  Authors: Yu Miao, Li-Min Liu, Feng Qi,  
  Keywords: Inequality, Exponential of sum, Nonnegative sequence, Normal random variable.  
  Date Received: 12/11/07  
  Date Accepted: 07/03/08  
  Subject Codes:

26D15; 60E15

  
  Editors: Anthony Sofo,  
 
  Abstract:

Using probability theory methods, the following sharp inequality is established:

$displaystyle frac{e^k}{k^k} left(sum_{i=1}^nx_iright)^{k}leexpleft(sum_{i=1}^n x_iright),$    
where $ kinmathbb{N}$, $ ninmathbb{N}$ and $ x_ige 0$ for $ 1le ile n$. Upon taking $ k=2$ in the above inequality, the inequalities obtained in [F. Qi, Inequalities between the sum of squares and the exponential of sum of a nonnegative sequence, J. Inequal. Pure Appl. Math. 8(3) (2007), Art. 78 are refined. ;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=985