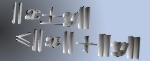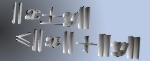| |
|
|
| |
Volume 1, Issue 1, Article 1 |
|
|
|
|
|
| |
Power-monotone sequences and Fourier series with positive coefficients
|
| |
|
Authors: |
Laszlo Leindler, |
|
| |
|
Keywords:
|
Fourier series, Fourier coefficients, Lipschitz classes, modulus of continuity, cosine and sine series, quasi power-monotone sequences |
|
| |
|
Date Received:
|
11/09/99 |
|
| |
|
Date Accepted:
|
01/12/99 |
|
| |
|
Subject Codes: |
26A16,26A15,40A05,42A16
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
J. Németh has extended several basic theorems of R.P. Boas Jr. pertaining to Fourier series with positive coefficients from Lipschitz classes to generalized Lipschitz classes. The goal of the present work is to find the common root of known results of this type and to establish two theorems that are generalizations of Németh’s results. Our can be considered as sample examples showing the utility of the notion of power-monotone sequences in a new research field.
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|