JIPAM

On an Opial Inequality with a Boundary Condition  
 
  Authors: Man Kam Kwong,  
  Keywords: Opial inequality, Integral condition, Calculus of variation.  
  Date Received: 01/11/06  
  Date Accepted: 08/03/07  
  Subject Codes:

26D10, 26D15.

  
  Editors: Don B. Hinton,  
 
  Abstract:

R.C. Brown conjectured (in 2001) that the Opial-type inequality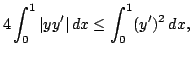

$ displaystyle 4 $ int_{0}^{1} $ vert yy^{$ prime }$ vert dx $ leq $ int_{0}^{1} (y^{$ prime})^2 dx , $
holds for all absolutely continuous functions $ y:[0,1]$ rightarrow $ mathbb{R} $ such that $ y^{$ prime}$ in L^2$ and $ $ int_{0}^{1} y dx=0 $. This was subsequently proved by Denzler [3]. An alternative proof was given by Brown and Plum [2]. Here we give a shorter proof.;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=817