JIPAM
| Some Inequalities Associated with a Linear Operator Defined for a Class of Analytic Functions | ||||
| Authors: | S. R. Swamy, | |||
| Keywords: | Analytic functions, Differential subordination, Ruscheweyh derivatives, Linear operator. | |||
| Date Received: | 07/03/05 | |||
| Date Accepted: | 25/07/05 | |||
| Subject Codes: |
30C45. |
|||
| Editors: | Herb Silverman, | |||
| Abstract: |
In this paper, we give a sufficient condition on a linear operator 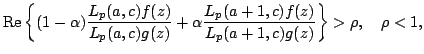 , implies , implies  | |||
http://jipam.vu.edu.au
The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=642