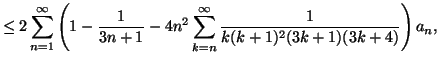JIPAM

Note on the Carleman's Inequality for a Negative Power Number  
 
  Authors: Thanh Long Nguyen, Vu Duy Linh Nguyen, Thi Thu Van Nguyen,  
  Keywords: Carleman's inequality.  
  Date Received: 30/10/02  
  Date Accepted: 25/11/02  
  Subject Codes:

26D15

  
  Editors: Hüseyin Bor,  
 
  Abstract:

By the method of indeterminate coefficients we prove the inequality

$displaystyle sum_{n=1}^{infty }frac{n}{frac{1}{a_{1}}+frac{1}{a {2}}+...+frac{1}{%% a_{n}}}$

$displaystyle leq 2sum_{n=1}^{infty }left( 1-frac{1}{3n+1}%% -4n^{2}sum_{k=n}^{infty }frac{1}{k(k+1)^{2}(3k+1)(3k+4)}right) a_{n}, $

where $ a_{n}>0, n=1,2,... sum_{n=1}^{infty }a_{n}<infty .$;


This article was printed from JIPAM
http://jipam.vu.edu.au

The URL for this article is:
http://jipam.vu.edu.au/article.php?sid=238