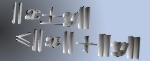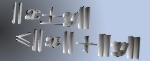| |
|
|
| |
Volume 9, Issue 3, Article 69 |
|
|
|
|
|
| |
On Integrability of Functions Defined by Trigonometric Series
|
| |
|
Authors: |
Laszlo Leindler, |
|
| |
|
Keywords:
|
Sine and cosine series, $L^p$ integrability, equivalence of coefficient conditions, quasi power-monotone sequences. |
|
| |
|
Date Received:
|
15/01/08 |
|
| |
|
Date Accepted:
|
19/08/08 |
|
| |
|
Subject Codes: |
26D15, 26A42, 40A05, 42A32.
|
|
| |
|
Editors: |
Sever S. Dragomir, |
|
| |
|
|
|
|
|
| |
|
Abstract: |
The goal of the present paper is to generalize two theorems of R.P. Boas Jr. pertaining to  integrability of Fourier series with nonnegative coefficients and weight integrability of Fourier series with nonnegative coefficients and weight  In our improvement the weight In our improvement the weight  is replaced by a more general one, and the case is replaced by a more general one, and the case  is also yielded. We also generalize an equivalence statement of Boas utilizing power-monotone sequences instead of is also yielded. We also generalize an equivalence statement of Boas utilizing power-monotone sequences instead of  . .
|
|
|
|
|
|
| |
|
|
|
|
| |
|
|
|
|
|