Let
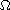 be a bounded domain in
be a bounded domain in
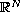 ,
,
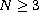 ,
and
,
and
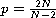 the limiting Sobolev exponent.
We show that for
the limiting Sobolev exponent.
We show that for
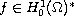 , satisfying suitable
conditions, the nonlinear elliptic problem
, satisfying suitable
conditions, the nonlinear elliptic problem
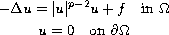
has at least three solutions in
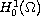 .
.
Samira Benmouloud, Mostafa Khiddi, Simohammed Sbai
Abstract:
Let
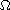 be a bounded domain in
be a bounded domain in
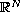 ,
,
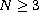 ,
and
,
and
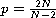 the limiting Sobolev exponent.
We show that for
the limiting Sobolev exponent.
We show that for
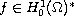 , satisfying suitable
conditions, the nonlinear elliptic problem
, satisfying suitable
conditions, the nonlinear elliptic problem
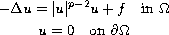
has at least three solutions in
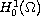 .
.
Published September 20, 2006.
Math Subject Classifications: 35J20, 35J65.
Key Words: Semilinear elliptic equations; critical Sobolev exponent.
Show me the DVI(31K), PDF(183K), TEX and other files for this article.
 |
Samira Benmouloud E.G.A.L, Dépt. Maths, Fac. Sciences Université Ibn Tofail, BP. 133, Kénitra, Maroc email: ben.sam@netcourrier.com |
|---|---|
| Mostafa Khiddi E.G.A.L, Dépt. Maths, Fac. Sciences Université Ibn Tofail, BP. 133, Kénitra, Maroc | |
 |
Simohammed Sbai E.G.A.L, Dépt. Maths, Fac. Sciences Université Ibn Tofail, BP. 133, Kénitra, Maroc email: sbaisimo@netcourrier.com |
Return to the table of contents for this conference.
Return to the EJDE web page