English version

Die rein geometrische Kreisquadratur init Zirkel und Lineal hat sich längst als nur annähernd möglich erwiesen. Weil aber die Kreiszahl Pi mit p = 3,14159265... bekannt ist, lässt sie sich trotzdem als Strecke und sogar als Kreis- oder Quadratfläche darstellen. Die Kreisflächenzahl lautet pr², die Quadratflächenzahl lautet [root(pr²)]² = [r(root-p)]². Mit dem Kreisradius r = 1 werden die Kreisfläche und die Quadratfläche DEFG gleich p. Im nachstehenden Bild sei die Einheitsstrecke 5 cm lang. Das Einheitsquadrat umfasst deshalb 5² = 25 cm². Das Grossquadrat NOPQ hat die Fläche 2² = 4 (bzw. 10² = 100 cm2). Die Flächen der Kreiszahl p sind also kleiner. Die Quadratfläche DEFG = p dient dem Lehrsatz a²+b² =c² des Pythagoras (L.d.P.) für Rechtwinkeldreiecke, denn zwei Flächen (Quadrat DEFG und Quadratring bzw. Kreis- und Summe der 4 Restflächen) addieren sich zur Fläche NOPQ. Es gilt [5(root-p)]²+ [5(root(4- p))]²= 25(p +4-p) = 100.

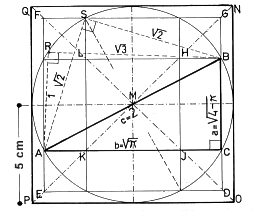
Der Inkreis des Grossquadrates umschliesst das Rechtwinkeldreieck ABC=a:b:c = root(4 - p) : root(p : 2). Der L.d.P. bestätigt (4 - p) + p = 4, er gilt auch für "irrationale" Rechtwinkeldreiecke. Lässt man den Punkt C auf seinem Halbkreis zwischen A und B wandern, dann sind alle möglichen, also unendlich viele, Rechtwinkeldreiecke bzw. Rechteck-Halbformen erfasst. Die Summe der jeweils zwei zugehörigen Kathetenquadrate ist stets gleich 4. (Für ABS gilt 2(root-2)² = 4, für ABR gilt 1²+(root-3)² = 4.) Weil alle ebenen Dreiecke einen Umkreis berühren, sind ihre Formen im Kreisquadraturbild vertreten. Es handelt sich also um ein wahrhaft "kosmisches Arrangement". Man kann ja sogar einen Sternenhimmel auf eine Kreisfläche projizieren! Andererseits ist der Kreis mit Radius 1 auch Inkreis im Rechtwinkeldreieck 3:4:5. Wegen der Bildquadratfläche 100 könnte man 3:4:5 auf 6:8:10 verdoppelt in den Kreis zeichnen, denn 6² +8²=10² bzw. 36+64=100. Hier wird eine Verbindung zum unendlichen System der "primitiven Pythagorastripel" (p.P.T).erkennbar, welche alle natiirlichen und sogar alle positiven reellen Zahlen erfassen.

Die unendlich vielen, variablen, im Kreis möglichen Dreiecke wie ABC kann man paarweise verdreht zu zweiachsig symmetrischen Rechtecken und zu einachsig symmetrischen Drachenvierecken (Deltoiden) zusammenlegen. Die letzteren entstehen durch Herumklappen des Dreiecks ABC um AB. Rechtecke und Deltoide werden als symmetrische Kreisvierecke bezeichnet.. Die Flächen ACBR und ACBS sind unsymmetrische Kreisvierecke. Je zwei gleiche Rechtecke bilden die "Balken" eines Griechenkreuzes, dessen Aussenecken auf dem Kreis ein vierachsig symmetrisches Achteck markieren. Oktogone sind acht- achsig zentralsymmetrisch. Die Fläche des "Kreuzbalkenschnittquadrates" HJKL gleicht der schmalen Rahmenfläche zwischen NOPQ und DEFG. Deshalb entspricht die Fläche p auch der breiten Quadratringfläche zwischen NOPQ und HJKL. Die Beziehung gilt immer. Griechenkreuze erleichtern das Erkennen vieler Flächen- und Zahlenbeziehungen zwischen allen ebenen Dreiecken, also auch zwischen den anderen Vielecken, und der Kreisquadratur. Wichtigste Hilfsmittel sind die Strahlensätze und der für Rechtwinkeldreiecke mehrhundertfach bewiesene L.d.P.. Diese Hilfsmittel gelten nach Anpassung für alle ebenen Dreiecke einschliess1ich der berühmten, irrationalen "Fermatdreiecke" nach Pierre de Fermat (1601-1665). Der erstaunliche letzte Satz bedarf bewiesener geometrischer und zahlentheoretischer Erläuterungen. Ein Sonderfall ist das zentralsymmetrische Sechseck (Hexagon, Davidstern) mit den Seiten 1 = r, der einfachsten Fermatgleichung 1ⁿ + 1ⁿ = 2 und mit dem gleichseitigen Dreieck als "Gottesauge".

LITERATUR:
Schröer, Klaus and Klaus Irle . "Ich aber quadriere den Kreis..." (Münster: Waxmann Verlag, 1998). Jetzt kaufen von Amazon.de, click here. Oder, lesen die Rezension des Buches von Gert Sperling in the NNJ, vol. 2 no. 1.

Dr. Helmut Sander, *14-02-20 in Kassell; Abitur 1938, 1938-45 Kriegseinsatz; 1946-50 Architekturstudium an der TH Hannover; danach tätig bei hessischen Stattsbauämtern und dem Hochschulbauamt Kassel und im Denkmalschutz, bes. für das Herkules-Bauwerk in Kassel-Wilhelmhoehe. Dazu 1981 Dissertation an der Techn. Universtät Berlin (ISBN 3-87816-037-2). Seit 1948 kunstwissenschaftliche und zahlentheoretisch-geometrische Studien. Er veröffentlichte 25 Aufsaetze in Fachzeitschriften zur Belebung und Erweiterung der Lehren des Pythagoras und ihrer Elementarisierung für Arithmetik und Geometrie.

RELATED SITES ON THE WORLD WIDE WEB

Squaring the Circle
Squaring the Circle: Hobbes on Philosophy and Geometry
Squaring the circle using a special kind of polygon
The Number Pi

Copyright ©2000 Kim Williams